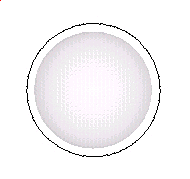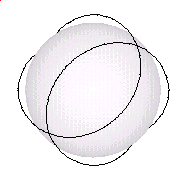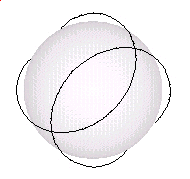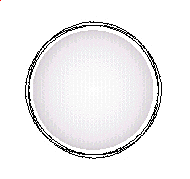
Again, here is a GIF movie showing the pattern "breathing".

Note how the sphere in the center is expanding and contracting.
Although these images show the pattern in one fixed orientation, it is assumed that "in reality" the pattern is always spinning about. The pattern would then define a sphere. The sphere defined by the pattern would also expand and contract just as the sphere in the center of the above movie expands and contracts.
The question to be answered then is: "What is the radius of the pattern defined spheres when the pattern is fully open and when the pattern is in its 'closed' hoop (circle) position?"
There are (at least) two answer. The first answer is for the case that the overall length of the can change. That is, if a model of the pattern were made out of "wire" then the wire would stretch and contract as it is opened and closed. The second answer is for the case in which the pattern always has a fixed total length. That is, the "wire" can not stretch or contract.
We constructed the pattern on the tetrahedron in another section. Recall that we drew a circle inside each of the tetrahedron's 4 trianglular faces.
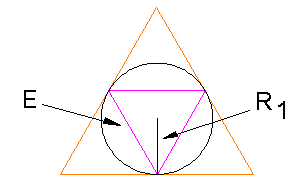
The radius of the circle is R1 = 1/sqrt(3)E = 0.5773503 (approx.). ("E" is the edge length of the triangle around which the circle is drawn.) This is the radius of the "hoop" when the pattern is in its "closed" position.
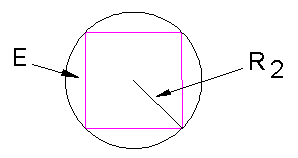
However, in the maxium open position, the 4 circles are drawn around an octahedron which also has an edge length of E.

The octahedron consists of 3 interesting squares.
the squares have an edge length of E. So the
sphere defined by the octahedron (the pattern in its open position)
will have a radius of
R2 = 1/sqrt(2)E = 0.70710678 (approx.).
So, the pattern defined spheres expand from 1/sqrt(3)E to 1/sqrt(2)E. That is, the ratio of contraction is sqrt(2)/sqrt(3) = 0.8164966(approx.).
We note that with the circumscribed sphere around a VE (cuboctahedron) having a radius of E (edge length of the VE) then the inscribed sphere which just touches the center of the 8 triangular faces of the VE will have a radius of sqrt(2)/sqrt(3)E. This is in the same ratio as the pattern defined sphere's.
In this case, if we set the radius of the pattern to be 1 when in its closed form, then the radius of an arc when in the fully open position will be
arc-ro = 9/8.
However, in the open position, the 4 arcs define an octahedron. The distance from the octahedron's center of volume to a vertex (through which the pattern's arcs pass) is given by
sphere-ro = sqrt(3/2)(9/8), (approx. 1.3778)
In this case, the closed shpere of radius 1 "opens" to a sphere of radius sqrt(3/2)(9/8), (approx. 1.3778).
If the open sphere radius is defined to be 1 then the closed sphere radius will be sqrt(2/3)(8/9), (approx. 0.7258).
Usage Note: My work is copyrighted. You may use my work but you may not include my work, or parts of it, in any for-profit project without my consent.