A Natural Construction For The Dimpled 120 Polyhedron

I here show a way to construct the 120 Polyhedron and I show how the "dimpled" aspect of the 120 Poly comes about in a "natural" way.

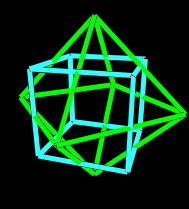
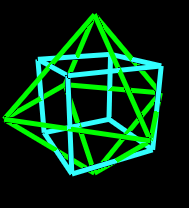
First, consider the cube and the octahedron. They are dauls of each other. Here are some pictures.

Notice that I picked the relative size of the cube and the octahedron so that their edges intersect each other. This can be used to define the Rhombic Dodecahedron. However, we are not going to need the Rhombic Dodecahedron for what I am trying to show. I show it here in order to demonstrate how duals can define another polyhedron.

Next, consider the Icosahedron and the Regular Dodecahedron. They are duals of each other. And we again pick the relative size for each polyhedron such that their edges intersect each other.

We now use the Icosahedron and Regular Dodecahedron to define the Tricontahedron. (This is simalar to the construction of the Rhombic Dodecahedron from the Cube and the Octahedron above.)

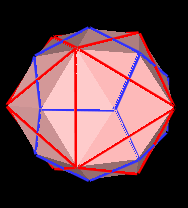
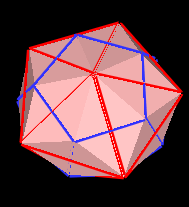
Now, it is perhaps not well known, but the cube "fits" into the Regular Dodecahedron exactly. That is, for the correct size and orientation, the cube and the Regular Dodecahedron share the same 8 vertices.

This gives us a scale and orientation so that we can fit the cube and the octahedron into the Icosahedron and the Regular Dodecahedron. The results look like this:

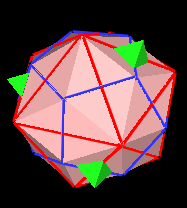
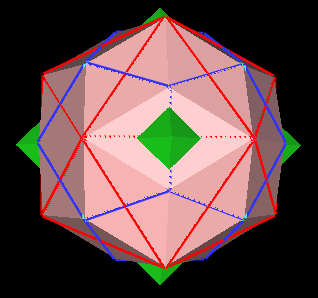
Now, the tricontahedron has 30 diamond faces. If we could somehow replace each diamond face with four triangular faces, then the resulting polyhedron would have 30 x 4 = 120 triangular faces.

Note that each of the diamond faces of the Tricontahedron have a red and a blue line on them. These lines intersect and divide the diamond faces into 4 triangles.

Next note that the green octahedron "sticks out" through 6 (out of 30) of the diamond face centers of the Tricontahedron. If we imagine that all the diamond face centers are pushed radially outward to the Octahedron vertices, we end up with a "dimpled" 120 polyhedron.

Here I have outlined 3 of the diamond faces. The diamond face centers are all "pushed out".

This new construction for the "dimpled" 120 polyhedron seems more "natural" than the previous method. The previous construction failed to show or explain how the dimpling comes about. We simply dimpled the 120 poly because we were told to. The degree of dimpling was, therefore, always in question. This construction shows how the dimpling comes about as relations to all the other polyhedra involved.

Usage Note: My work is copyrighted. You may use my work but you may not include my work, or parts of it, in any for-profit project without my consent.