Storyboard
This is a "storyboard" detailing the geometry and dynamics that
Lynnclaire Dennis describes based on her near death experiences.
- Formation of the Geometry
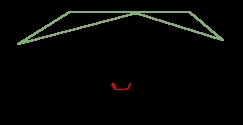
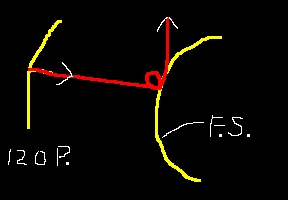
- There are two "objects" which can be seen. From a distance
they seem to be a "line" and a "point".
- When looking from one point of view one sees what looks
like a "line" over a "point". Change the perspective and
you see a point above a line. Change the perspective
and you see a point beside a line. Change the perspective
again and you see an 'X'.



- The "top" object, the 120 Icosahedron bubble, forms, growing
downward where it eventually circumscribes the "bottom" object,
the 144 "hyperdiamond" Octa.
- The Octa also begins to form, growing upward to eventually
define the 144 Polyhedron.
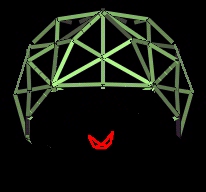
- The "top" Icosa encloses the Octa embedding it within
what is about to be defined as the 120 Polyhedron. At this
point the Octa is still forming, growing upward within
the Icosa.
- As the 120 Icosa bubble closes, there is an "upward" push
on the Octa centering it within the 120 Polyhedron. The
144 Octa based Polyhedron has not completely formed at
this time.

- There is a "hot" center inside the Octa which grows in
intensity as the 144 polyhedron is forming.
- The Octa object completes its formation
into the 144 polyhedron and closes at the "North".
There is an imploding "spark" at its center, which is
pushed out to the vertices of the 144. This spark
igniting the initial generation of the original 48 energy beams.

- Energy Beams out of the 144 Poly
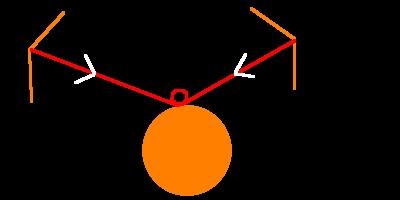
- 48 energy beams come out of the 144 Polyhedron at 48 vertices in 8
groups comprised of 6 beams each.

- The straight energy beams have a "Y" cross section and move radially out
from the 144 Poly.
- They go out to the "Focusing Sphere".
- After these beams get emitted, the 144 Polyhedron starts
to spin.
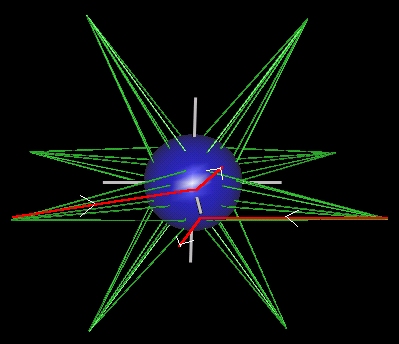
- Energy Beams out of the Focusing Sphere
- The "Focusing Sphere" does not have a polyhedral
(faces, vertices) structure. It is a sphere.

- As the 48 energy beams pass through the Focusing Sphere,
they get bent (focused). This curvature is due to the now
spinning 144 polyhedron.



- After the energy beams get bent, they are again straight,
"Y" cross section shaped beams.
- The bending is such that the 48 beams form 8 groups of
6 beams each. Each group (or bundle) gets focused into a
different vertex of the 120 Polyhedron.

- The 120 Polyhedron is a "mixed" polyhedron being
both concave and convex. (That is, the surface has "hills" and
"valleys".)
- There are 48 / 6 = 8 such "bundles" being focused into
8 of the 120 Poly vertices.
- The vertices that these 8 bundles get focused into correspond
to 8 (out of 12) vertices of the Icosahedron (which is the
base polyhedron forming the 120 Polyhedron.
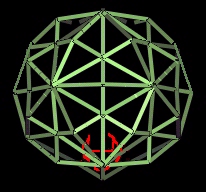
- The grouping of the energy beams can be identified by refering
back to the 144 Polyhedron. A group is identified
in the next illustration by yellow dots.

- There are 4 vertices of the Icosahedron which do not have
energy beams focused into them. These 4 vertices are in the
same plane and therefore form an "equator". The 4 vertices
are on the same great circle.
- From the 120 Poly Back to the Focuing Sphere
- The energy beams get bounced back from the 120 Poly (from
the 8 Icosahedon vertices) back to the Focusing sphere.
- There are 8 energy beams coming back from the 120 Poly to the
Focusing sphere. One energy beam from each of the 8 vertices
involved in the bounce back.
- These 8 energy beams are straight unitl
they approach the Focusing sphere.
- The 8 energy beams have a "Y" cross section.
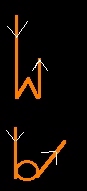
- At the focusing sphere, the energy beams do a small
loop and ricochet off the focusing sphere. The little loop
is like a cursive "e".
- The energy beams on "opposite" sides, coming in from opposite
vertices, seem to hit the Focusing sphere at approximately the
the same point.
- But they actually pass by each other.
- The loop is like a cork screw.
- Back to 120 Poly and Other Ricochets
- The 8 energy beams now go back to the 120 polyhedron and
begin ricochetting around the inside of the 120 Poly.
- The energy beams, in repeated bouncing around, remain
straight.
- At some point the 8 energy beams synchronize to form the Pattern knot
in the "open" 19.5 degree position.
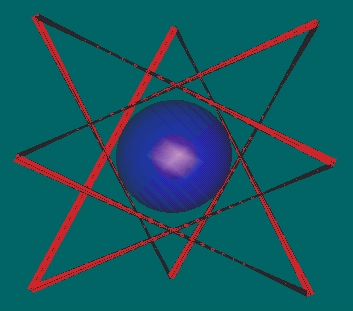
- Because the 120 Polyhedron is "dimpled in" at the 20 vertices
corresponding to the Icosahedron's face centers, the interior
surface of the 120 Polyhedron is not smooth. The inward
dumps of the 120 Poly channel the energy beams into the
straight edge pattern formation. (Perhaps as lens refract
light.)
- The Pattern knot at this point consists of 8 straight energy
beams.
- Note that the 8 vertices of the straight edge Pattern knot
are not all at the same distance from the center of volume.
This is because 4 out of the 8 vertices of the straight
edge Pattern knot are at the "dimpled in" Icosa face centers.
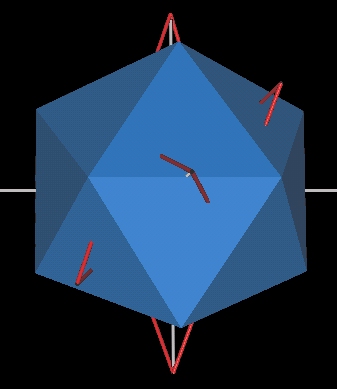
- The other 4 vertices of the straight edge Pattern knot are
at 4 vertices of the 120 Poly corresponding to mid-edges
of the Icosahedron. Note that these 4 vertices (mid-edge
points of the Icosahedron) are all in the same plane. They,
therefore, are on the same great circle equator of the
120 Poly.
- Formation of Vesica Pisces
- The energy beam is squashed flat. Looks like a line from one orientation.

- From another orientation, it looks like the Vesica Pisces.

- The 120 Polyhedron is distorted into an ellipse at this time.
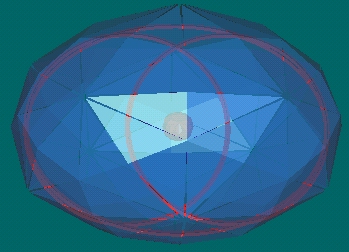

- And the Pent vertices of the 120 Polyhedron opens. (The pentagon
like face is outlined in orange. The vertex at the center of
this pentagon is open a little bit.)
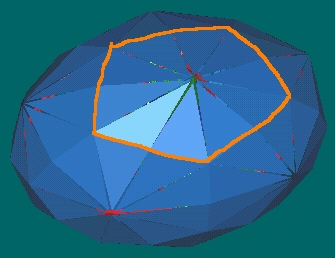
- The triangles making up the surface of the 120 Polyhedron
can also be grouped into diamonds
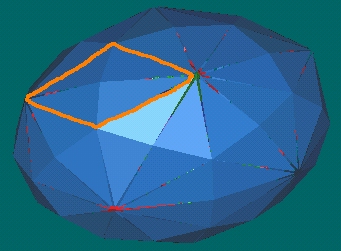
as well as triangles.
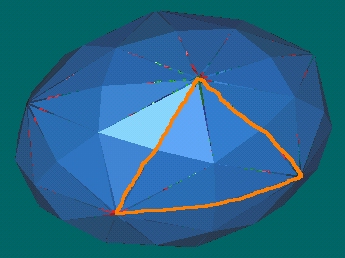
- 19.5 Degree Pattern
- The vesica pisces form "opens" into the 19.5 degree Pattern knot.
The curved Pattern knot is formed.

- There is a 720 degree (3/2) twist to the "Y" coss sectioned
energy beam of the Pattern knot. As if someone cut the
"ribbon", gave it a 720 degree twist and glued it back together.
- The 120 Polyhedron is spherical (and concave/convex) again.
- The 120 Poly starts to spin as it returns to a spherical
shape.
- The spin is in the opposite direction of the 144 Polyhedron
and such that when the 120 Poly is again in the ellipsoid
shape, it is spinning about the ellipsoid's long axis.
- The Pattern knot rotates on an asymmetric axis at a 22.5 degree
angle of asymmetry.
- Formation of Vesica Pisces Again
- The Pattern knot, in the 19.5 degree position, then
squashes flat again to form the Vesica Pisces.
- And passes through itself to form the Pattern knot in the
19.5 degree position in the opposite orientation.
- Energy Beams Through the 120 Poly
- Every time the Pattern knot is in the Vesica Pisces
poistion the 12 Icosa vertices of the 120 Polyhedron open
up a little.
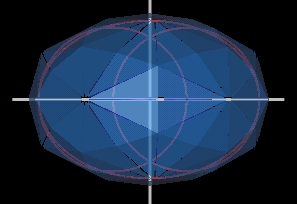
- Through each of the 12 openings a single energy beam emerges.
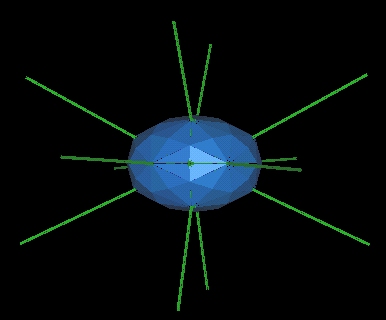
- The structure of the beam has a "Y" cross section.
- The 120 Polyhedron is rotating. It started rotating as the
Pattern knot was first formed. That is, as the formation of
the Vesica Pisces changed into the 19.5 degree open Pattern knot.
- Curve Back to the 120 Poly
- The 12 energy beams bends around and returns to the 120 Polyhedron.
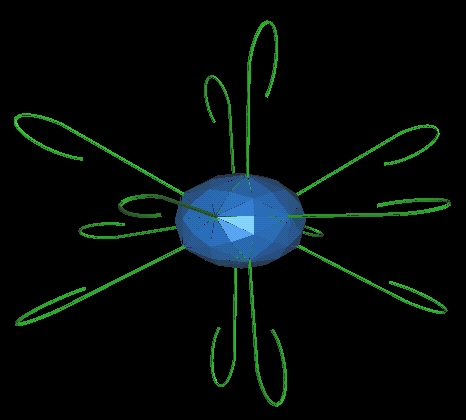
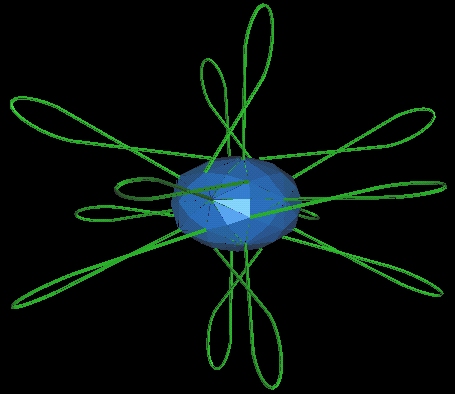
- During the "loop back", each of the 12 loops spwans a bubble.
- There is a "twisting" to this loop back.
- The 12 energy beams enter the 120 Poly through the face
center of
the Icosa triangles of the 120 Polyhedron. There is a "closed"
vertex at these points.
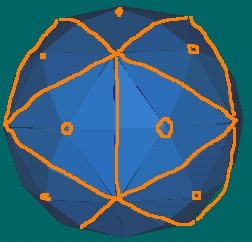
- There are 12 energy beams and 20 Icosa face centers. So there
are (20 - 12) = 8 Icosa face centers which do not have
energy beams returning into them. These 8 Icosa
face centers can be grouped into 2 groups of 4 face centers.
There is one group of 4 at each "end" of the 120 Poly ellipsoid.
Therefore, the energy beams do not return into the ellipsoid
ends. A group of 4 face centers can be identified as follows
(using the Icosahedron):
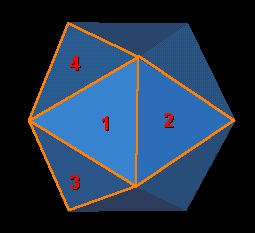
- And a similar grouping on the reverse side of the Icosa. This
grouping results in a edge-bond connected band of 12 triangles
around the Icosa. This "band" of triangles is then around the
ellipsoid "equator", although the band oscillates from being
a little below to a little above the "equator."
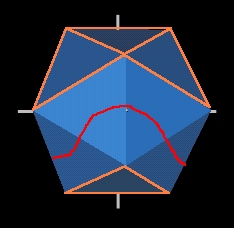
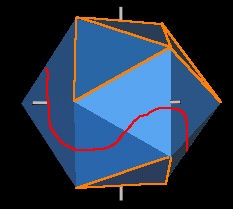
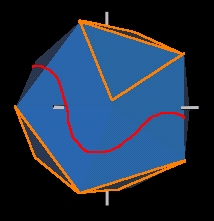
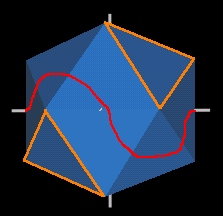
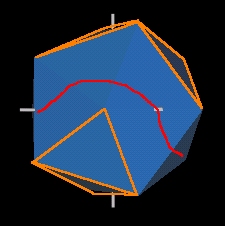
- Note that the major axis of the ellipsoid is not through 2 Icosa face
centers but through 2 Icosa edges.
- The "triangular vertices" (Icosa face centers) become dimpled
as the 120 Poly becomes spherical resulting in the 120 Poly
becoming a mixed convex/concave polyhedron.

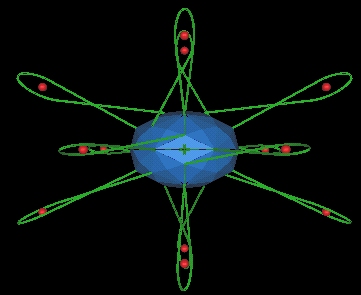
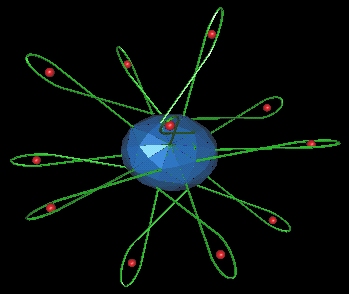
- Progression of Bubbles
- The 12 bubble spheres each produce another 12 spheres.
- There is a progression of bubble spheres until there is
one plus twelve times 13 to the 5th. [(1+12)*13^5]
Usage Note: My work is copyrighted. You may use my work but
you may not include my work, or parts of it, in any for-profit
project without my consent.











































