The Vesica Pisces and Interseting 120 Polyhedra

Consider 2 intersecting 120 Polyhedra.

2 Intersection 120 Polyhedra

The intersection is such that all the vertices at the interescting plane "A" match and such that a vertex of one of the 120 Polyhedra is at the center of volume of the other 120 Polyhedron ("B" and "C").

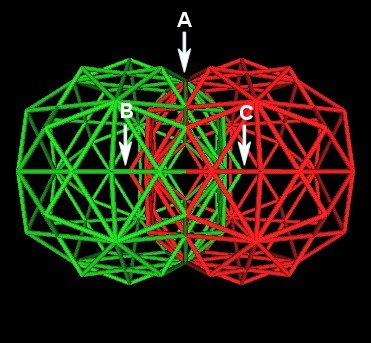
Vertices Match Just Right

We can rotate the image a little bit and trace out the resulting Vesica Pisces.

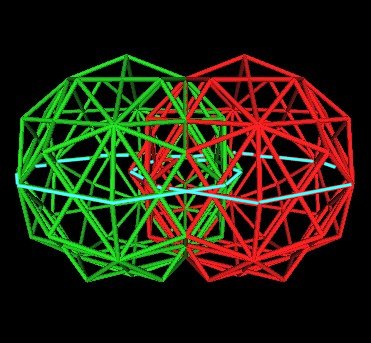
Vesica Pisces in Intersecting 120 Poly

Actually, there are 2 Vesica Pisces at 90° to each other.

2 Vesica Pisces in Intersecting 120 Poly

This is all a result of the 120 Polyhedra being constructed from Octahedra.

Intersecting Octahedra in Vesica Pisces position

Note that the part of the V.P. circle inside the other circle spans 120°.

Arc measurement inside V.P.

If, for some reason, we can subtract this part of the whole circle we are left with a 240° arc. For a V.P., there are 2 circles. From each we remove the 2 inner arcs of 120°.

Inner Arcs removed from V.P.

But we just showed there are 2 Vesica Pisces in the intersecting 120 Polyhedron.

So we have 4 arcs of 240° each.

But this is just a description of the Pattern Knot.

See Constructing The Pattern From A Tetrahedron in which I showed the construction of the Pattern knot from 4 circles drawn on the 4 faces of a Tetrahedron. For each circle, an arc of 120° is removed.

I had hoped that these thoughts on the Vesica Pisces in the 120 Polyhedron might lead to a new way to construct the Pattern knot, but I don't see how.

I also thought this was all new, but I find that I did something similar sometime ago with the 144 Polyhedron. See a Note I wrote to Lynnclaire some time ago.