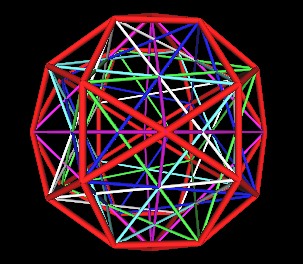
Marvin reports (03-03-04) to me that "The ratio of the edge length of the compound five icosas to the edge length of the 30 verti is Phi." (Phi is the Golden Ratio.)
Let us calculate this.
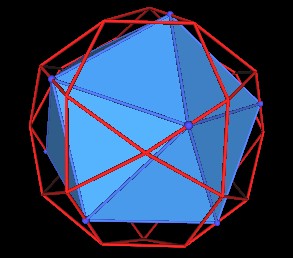
Recall that the matrix of 5 intersecting Octahedra define the vertices of the 30-Verti.

Take away the 30-Verti
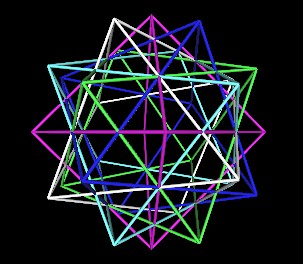
we have the 5 intersecting Octahedra.
One set of the edge-created intersecting points defines the Icosahedron.
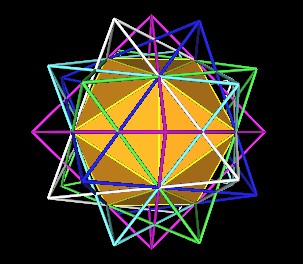
Take away all but one of the Octahedra, we get a better view of how the Icosahedron fits in the Octahedron.

Now, the triangular face of the Icosahedron is in the same plane as the triangular face of the Octahedron.
We define
DVE = Distance from center of volume to a mid-edge point,
DVF = Distance from center of Volume to a Face center,
DVV = Distance from center of Volume to a Vertex,
EL = Edge Length.
We know that
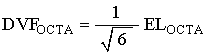
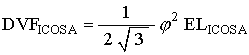
where
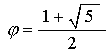
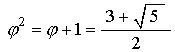
Since the Icosahedron triangle is in the plane of the Octahedron triangle, we have
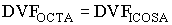
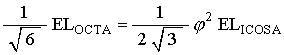
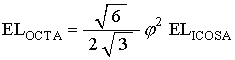
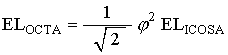
Which gives the Octahedron edge length in terms of the Icosahedron edge length.
We also have for the Octahedron
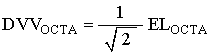
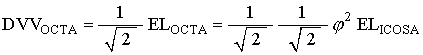

which gives the distance DVV for the Octahedron in terms of the Icosahedron edge length.
Now, we know that for the 30-Verti that

Because the vertices of the 30-Verti are the same as the vertices of the Octahedra, we have

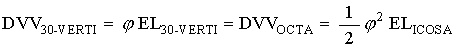
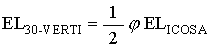
As I have mentioned before, there is another way to define an Icosahedron within the 30-Verti. This is to use the mid-edge points of the 30-Verti.
In this case, we get
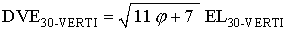

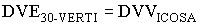
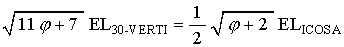
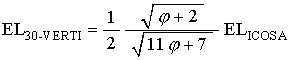
This equation might be simplified. But I don't have the time to do it at the moment....
This work is copyrighted, 2004 by Robert W. Gray.
You may not use any of this material, nor any material on our linked web pages,
without first obtaining written permission.