
The 30-Verti has 60 edges.

It is possible to position an Icosahedron in the 30-Verti by using the mid-edge points of 12 of the edges of the 30-Verti.

Because 60 / 12 = 5, one is lead to conjecture that you can fit 5 Icosahedra in the 30-Verti using only the 30-Verti mid-edge points. This is indeed the case.


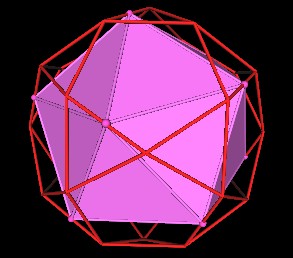
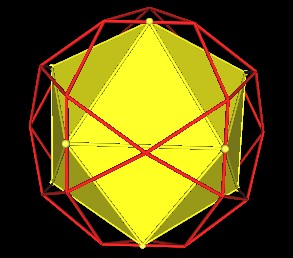

Here is an animation showing all 5 Icosahedra within the 30-Verti.
These are the 5 "alternate" Icosahedra in the corresponding 5 intersecting Octahedra.
Recall that dividing the edges of the Octahedron into Golden Ratio segments creates new vertices along the Octahedron's edges. Connecting these new vertices together defines an Icosahedron within the Octahedron.
But there are 2 different ways to divide an edge into Golden Ratio segments, depending on from which of the 2 ends of the edge you measure from.

In the above Figure, the white and blue Icosahedra show the 2 Icosahedra in an octahedron.
So, for every Octahedron, there are 2 Icosahedra within defined by cutting the Octahedron's edges into Golden Ratios.
Considering the matrix of 5 Octahedra, there are then 10 Icosahedra defined.
See "10 Icosahedra" for more detail on this.
5 of the Icosahedra become coincident with one another and can not be distinguished.
The remaining 5 "alternative" Icosahedra are distinguishable. And these are the 5 Icosahedra defined by the mid-edge points of the 30-Verti.

This work is copyrighted, 2004 by Robert W. Gray.
You may not use any of this material, nor any material on our linked web pages,
without first obtaining written permission.