
The study of the basic polyhedra is both a study in the properties of the space we live in as well as a source for basic design. Unfortunately, the relationships among the Platonic polyhedra (as well as some other basic polyhedra) are not taught as “basic knowledge” in the grade schools, nor in the Colleges and Universities. I will present an introduction to the basic polyhedra, showing how they are related to each other.
A new 120 triangular faced polyhedron will be introduced. It will be shown that this 120 Polyhedron provides a unifying vertex coordination for all of the polyhedra to be introduced.
The "Jitterbug", a dynamic polyhedron, will be demonstrated. It will be shown that the Jitterbug motion provides a dynamic means for defining these polyhedra and is, therefore, of fundamental importance to the dynamics of space itself.
The Golden ratio will be seen to occur throughout the polyhedra's relationships. This is both a fascinating "coincidence" of space as well as a visually pleasing source for basic design work.
|
|
|
|
| Tetrahedron | Octahedron |
|
|
| Cube |
|
|
|
| Dodecahedron | Icosahedron |
Three kinds of symmetry rotation axes (see above illustrations for examples):
If a rotation of a polyhedron about a particular axis by an angular amount
For example, the Tetrahedron's mid-edge to mid-edge axes: A rotation by 180° puts the Tetrahedron in the same positions as no rotation at all. Therefore, for this polyhedron and for this rotation axis, the Tetrahedron is 360° / 180° = 2-fold symmetric.
Neither the Tetrahedron nor the Octahedron can fill all of space, without intersection, such that
The Tetrahedron and the Octahedron can combine face to face to fill all space with Tetrahedra and Octahedra.
The Cube can fill all space by itself.
Neither the Dodecahedron nor the Icosahedron can fill all space, singly or in combination.
To create the "dual" of a polyhedron, replace faces with vertices, and vertices with faces. (The following illustrations show the polyhedra scaled so that the dual polyhedra's edges intersect each other.)
|
|
|
| Duals: Cube and Octahedron | Duals: Dodecahedron and Icosahedron |
|
|
| Self-Duals: Two Intersecting Tetrahedra |
When scaled as shown, the Cube and Octahedron dual pair define the Rhombic Dodecahedron (shown in green). The Rhombic Dodecahedron fills all space.
| Cube and Octahedron Duals Define Rhombic Dodecahedron |
The Icosahedron and the (regular) Dodecahedron dual pair define the rhombic Triacontahedron (shown in green).
| Icosahedron and Dodecahedron Duals Define Rhombic Triacontahedron |
The 2 intersecting Tetrahedra self dual pair define the Cube (shown in green).
| Tetrahedra Self Duals Define Cube |
| Name | Vertices | Faces | Edges | V + F | E + 2 |
| Tetrahedron | 4 | 4 | 6 | 8 | 8 |
| Cube | 8 | 6 | 12 | 14 | 14 |
| Octahedron | 6 | 8 | 12 | 14 | 14 |
| Rhombic Dodecahedron | 14 | 12 | 24 | 26 | 26 |
| Icosahedron | 12 | 20 | 30 | 32 | 32 |
| Dodecahedron | 20 | 12 | 30 | 32 | 32 |
| Rhombic Triacontahedron | 32 | 30 | 60 | 62 | 62 |
| Name | Sum of Angles 1 Face |
Faces | Total Sum of Surface Angles |
Vertices | V*360° | V*360°-720° |
| Tetrahedron | 60°*3=180° | 4 | 720° | 4 | 1440° | 720° |
| Cube | 90°*4=360° | 6 | 2160° | 8 | 2880° | 2160° |
| Octahedron | 60°*3=180° | 8 | 1440° | 6 | 2160° | 1440° |
| Rhombic Dodecahedron | 360° | 12 | 4320° | 14 | 5040° | 4320° |
| Icosahedron | 60°*3=180° | 20 | 3600° | 12 | 4320° | 3600° |
| Dodecahedron | 108°*5=540° | 12 | 6480° | 20 | 7200° | 6480° |
| Rhombic Triacontahedron | 360° | 30 | 10800° | 32 | 11520° | 10800° |
| Name | Volume Equation |
| Tetrahedron | 1 (Edge Length)^3 |
| Cube | 3 (Face Diagonal)^3 |
| Octahedron | 4 (Edge Length)^3 |
| Rhombic Dodecahedron | 6 (Long Face Diagonal)^3 |
| Icosahedron | 5sqrt(2)p^2(E.L.)^3 |
| Dodecahedron | (24+42p)(E.L.^3)/sqrt(2) |
| Rhombic Triacontahedron | 15sqrt(2)(E.L.)^3 |
We have just seen how two intersection Tetrahedra define a cube.
|
|
| Two Tetrahedra Define a Cube |
| Intersecting Tetrahedra Define Octahedron |
| Intersecting Cube and Octahedron Define VE |
| 10 Tetrahedra In The Dodecahedron |
Each of the Dodecahedron's vertices is shared with 2 Tetrahedra. We can eliminate this redundancy by removing 5 Tetrahedra.

|
| 5 Tetrahedra In The Dodecahedron |
This suggests a spiral vortex motion in each of the Dodecahedron's faces.
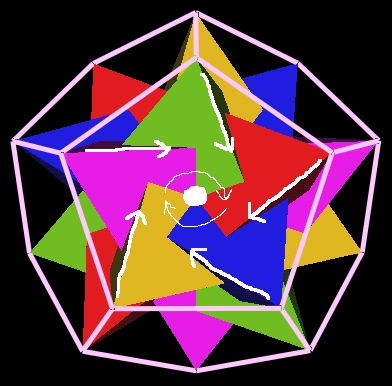
|
| 5 Tetrahedra In The Dodecahedron Suggests Spiral Motion |
It is possible to position 5 Cubes within the Dodecahedron.
| 5 Cubes In The Dodecahedron |
The model of 5 Cubes in the Dodecahedron suggested to me that the cubes might be positioned within the Dodecahedron by rotations from a single cube position. This is indeed the case.
Consider a single cube. It has 4 Vertex to Vertex rotation axes.
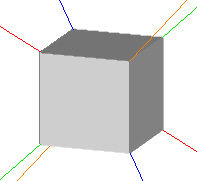
|
| 4 Vertex to Vertex Rotation Axes |
If we assign a Cube to each of these axes, we have a total of 5 Cubes (original 1 plus 4). We then rotate the 4 Cubes about these 4 axes.

|

|
| Four Rotating Cubes, One Stationary |
5 Cubes in Dodecahedron |
We will now put all of the polyhedra together into a single polyhedron. The resulting polyhedron will have 120 triangular faces. It is called the 120 Polyhedron.
This polyhedron was originally described to me by Lynnclaire Dennis. For more information on Ms Dennis and her work, see the Pattern web site at http://www.pattern.org/.
Start with the Dodecahedron.

|
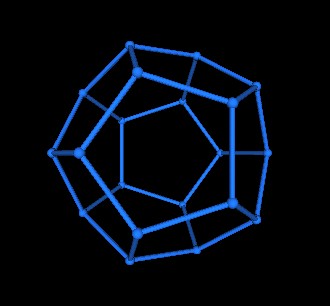
|
| Dodecahedron | |
Add in all 10 Tetrahedra.
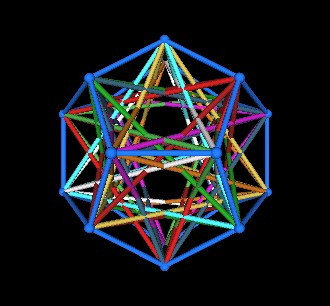
|

|
| Dodecahedron, Tetrahedra | |
Add the 5 Cubes.

|

|
| Dodecahedron, Tetrahedra, Cubes | |
Add the duals to each of the 5 Cubes; 5 Octahedra.
|
|
| Dodecahedron, Tetrahedra, Cubes, Octahedra | |
Recall that each Cube/Octahedron pair defines a rhombic Dodecahedron.
|

|
| Dodecahedron, Tetrahedra, Cubes, Octahedra, rhombic Dodecahedra | |
Add the dual to the (regular) Dodecahedron; the Icosahedron.

|
|
| Dodecahedron, Tetrahedra, Cubes, Octahedra,
rhombic Dodecahedra, Icosahedron |
|
Recall that the Icosahedron/Dodecahedron pair defines the rhombic Triacontahedron.

|

|
| Dodecahedron, Tetrahedra, Cubes, Octahedra,
rhombic Dodecahedra, Icosahedron, rhombic Triacontahedron |
|
Connect all the outer vertices together. This defines the 120 Polyhedron.

|
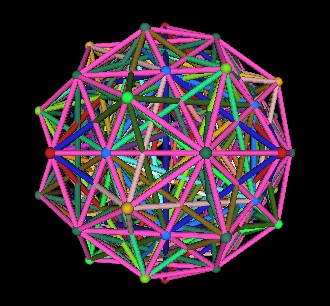
|
| Dodecahedron, Tetrahedra, Cubes, Octahedra,
rhombic Dodecahedra, Icosahedron, rhombic Triacontahedron, 120 Polyhedron |
|
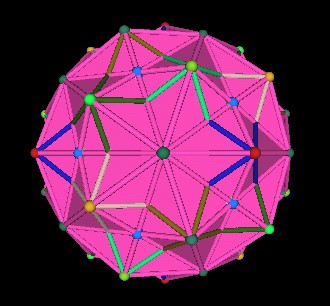
|
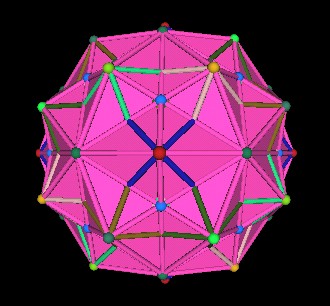
|
| 120 Polyhedron | |
(Note that there are other polyhedra with 120 triangular faces. They will not be discussed here.)
Recall the Cuboctahedron, which Fuller calls the "Vector Equilibrium" (VE).
| The VE |
With a Cuboctahedron (VE) constructed out of sticks and rubber vertices, Fuller often demonstrated what he called the "Jitterbug" motion. The Jitterbug shows how the VE can fold up into an Octahedron as well as how an Octahedron can expand in the VE.

|

|

|
| VE position |
Jitterbug in motion
|
Octahedron position |
The Jitterbug has 8 triangular faces. As these 8 faces rotate, they also move radially inward or outward from the center of volume along its 4 rotation axes.

|
|
Motion along 4 rotation axes
|
These are the same 4 rotation axes that we used to rotate the 4 cubes.

Jitterbug rotation axes |
Fuller pointed out that between the VE and the Octahedron positions, the Jitterbug will pass through an Icosahedron position.

|
|
Jitterbug defines the Icosahedron
|
If we allow the 8 rotating triangles to interpenetrate each other, then the Jitterbug can rotate and contract into two intersecting tetrahedra to define a cube.

|

|

|
| Jitterbug in Octahedron position |
Jitterbug in motion
|
Jitterbug in Cube position |
Further rotation and contraction results in the definition of another Icosahedron.

|

|

|
| Jitterbug in Cube position |
Jitterbug defines the Icosahedron
|
Jitterbug in Icosahedron position |
When the 120 Polyhedron is considered with all of its defining, internal polyhedra, many Jitterbugs can easily be identified. These Jitterbugs are not all in the same open position, nor of the same scale. Here is an illustration looking into the array of polyhedra through a regular Dodecahedron vertex. (The outer edges of the 120 Polyhedron are not shown.)

Looking into a Dodecahedron vertex |
In the next sequence of illustrations, I display various Jitterbugs by changing the associated polyhedron into a solid appearance. All of these Jitterbugs have the same face centered rotation axis passing through the regular Dodecahedron's vertex.

A Jitterbug in the Icosahedron position |

A Jitterbug defined by Cube edges |
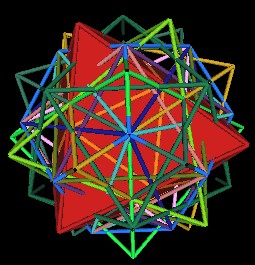
A Jitterbug in the Octahedron position |

A Jitterbug in the VE position |

A Jitterbug in the Tetrahedron position |
It is difficult to see the Jitterbug defined by the Cube's edges in the above illustration, so here is a different perspective. The Dodecahedron is shown with the 5 Cubes. Some of the edges of the Cubes are outlined in black. Filling in the triangular faces in black reveals the Jitterbug.

|

|
| A Jitterbug defined by the Cube edges | |
Notice the variation in the triangular face sizes and orientations. These variations show that there are many different Jitterbugs operating within the 120 Polyhedron.
The Octahedron is one position which the Jitterbug passes through. There are 5 Octahedra in the 120 Polyhedron. Here is a movie showing the dynamics of 5 Jitterbugs. Note that the Jitterbugs define both the Icosahedron and the Dodecahedron.

|
|
Five Jitterbugs passing through and
defining an Icosahedron and Dodecahedron |
Here are some additional combinations of polyhedra which I find particularly interesting.
| Ten Tetrahedra |
| Five Octahedra |

|
| Five Octahedra |
| Five Rhombic Dodecahedra |

|

|
| 5 Octahedra, Icosahedron, Dodecahedron | |

|
|
Surface waves over the 120 Polyhedron |
In order to calculate the properties of the 120 Polyhedron, it is helpful to first calculate the coordinates to its vertices. But what orientation and scale of the 120 Polyhedron should be used? Is there a preferred orientation and scale which will make calculations easier or which will highlight some important features of the 120 Polyhedron?
In a note published on "synergetics-l@teleport.com", Gerald de Jong showed that the regular Dodecahedron could be assigned simple coordinates expressed in terms of the Golden ratio. The Golden ratio is often represented by the Greek letter phi. However, I will use the letter "p" in this text. The Golden ratio is
which is approximately p = 1.618033989.
Gerald showed that the Dodecahedron's 20 vertices could all be assign numbers from the set
This is a remarkable set of numbers. For example, it can easily be shown that
In general, it can be shown that (for n an integer)
Additionally, using these numbers for the coordinates of the regular Dodecahedron highlights the Golden ratio aspects of the polyhedron.
Since the regular Dodecahedron's vertices are the same as 20 of the 120 Polyhedron's vertices, I will use Gerald's 20 coordinates to fix the orientation and scale of the 120 Polyhedron. I will then calculate and fill in the remaining 62-20=42 coordinates.
|
|
|
Remember that the 10 Tetrahedra, 5 Cubes, 5 Octahedra, 5 rhombic Dodecahedra, the regular Dodecahedron, Icosahedron and the rhombic Triacontahedron all share their vertices with the 120 Polyhedron. This means that all their vertex coordinates are a subset of the coordinates given above.
The combinations of 0, p, p^2, p^3 is very interesting.
Using the above coordinates, the basic data for the 120 Polyhedron can easily be calculated.
The 120 Polyhedron has 3 types of vertices. Each type of vertex is defined by the other polyhedra that share the vertex.

Vertex types |
| Vertex Type |
Shared With The Vertices Of |
| A | Octahedra, Rhombic Dodecahedra |
| B | Icosahedron, Rhombic Triacontahedron |
| C | Regular Dodecahedron, Rhombic Dodecahedra, Cubes,
Tetrahedra, Rhombic Triacontahedron |
The 3 different vertex types of the 120 Polyhedron are at different distances from the Polyhedron's center of volume.
| Vertex Label |
Radius | Approx. |
| A | 2p^2 | 5.236067977 |
| B | sqrt(2+p)p^2 | 4.97979657 |
| C | sqrt(3)p^2 | 4.534567884 |
The edge lengths of the triangular face ABC are
| Edge | Length | Approx. |
| AB | sqrt(3)p | 2.802517077 |
| AC | sqrt(2+p) | 1.902113033 |
| BC | sqrt(2+p)p | 3.077683537 |
The face angles are calculated to be
| Angle Label |
Angle | Approx. |
| BAC | arccos(1/(sqrt(6+3p)p)) | 79.18768304° |
| ABC | arccos((p^2)/sqrt(6+3p)) | 37.37736814° |
| ACB | arccos(p/(2+p)) | 63.43494882° |
The triangular face data is summarized in the following diagram.

Triangle Data |
In calculating the volumes of the polyhedra in the 120 Polyhedron, I will use, as Fuller does, the Tetrahedron as unit volume.
| Polyhedron | Coordinate Distance |
Normalized Length |
Volume | Approx. |
| Tetrahedron | Edge 2sqrt(2)p^2 |
1 | 1 | 1.0 |
| Cube | Face Diagonal 2sqrt(2)p^2 |
1 | 3 | 3.0 |
| Octahedron | Edge 2sqrt(2)p^2 |
1 | 4 | 4.0 |
| Rhombic Dodecahedron |
Long Face Diagonal 2sqrt(2)p^2 |
1 | 6 | 6.0 |
| Regular Dodecahedron |
Edge 2p |
1/(sqrt(2)p) | (3/2)(2+p) | 5.427050983 |
| Icosahedron | Edge 2p^2 |
1/sqrt(2) | (5/2)p^2 | 6.545084972 |
| Rhombic Triacontahedron |
Long Face Diagonal 2p^2 |
1/sqrt(2) | 15/2 | 7.5 |
| 120 Polyhedron | Long Face Diagonal of R. Triaconta. 2p^2 |
1/sqrt(2) | 15/p | 9.270509831 |
It is interesting to note that in the 120 Polyhedron, the Icosahedron edge length is equal to the Cube edge length. The Icosahedron edge length is also equal to the distance from the center of volume to an Octahedron vertex.
The Golden Ratio occurs quite frequently in biology. Many growth patterns exhibit the Fibonacci numbers (1, 1, 2, 3, 5, 8, 13, 21, etc.) in which the next number is the sum of the previous 2 numbers. The Fibonacci sequence is known to be connected with the Golden Ratio.
Although it is often pointed out that the Golden Ratio is the limit of successive Fibonacci numbers
this is also true for any sequence f(n) defined by
where f(n) is an integer for all n. The Fibonacci sequence (1, 1, 2, 3, 5, 8, 13, etc.) is just one such sequence. Any sequence as defined above will work.
The important point is that the Golden Ratio is not exclusively associated with the Fibonacci sequence, as many writings might lead you to believe.
For example, try f(1)=-23, f(2)=15, then f(3)=-8, f(4)=7, f(5)=-1, f(6)=6, f(7)=5, f(8)=11, f(9)=16, f(10)=27, etc. Then the limit as n approaches infinity of f(n+1)/f(n) will equal the Golden Ratio. (f(10)/f(9)=27/16=1.6875 which already starts to show the 1.6... of the Golden Ratio.)
So the Golden Ratio is connected with how the series is constructed and not a particular example of that construction (i.e. the Fibonacci sequence.) The Fibonacci sequence happens to be the most well known example of the construction rule
Returning to consider the coordinates of the 120 Polyhedron's vertices as listed above, it is obvious, from the z-coordinate, that the 62 vertices divide themselves into 9 groups. Each group defines a plane passing through the polyhedron. The spacing between the planes is shown in the next illustration.

Vertex layers in the 120 Polyhedron |
The central angles of the intersection of these planes with a circumsphere are given in the next table The results illustrate interesting relations between the angles and the Golden Ratio p. The radius of the sphere is 2p^2 = 2 + 2p.
| cos(18°) | sqrt(2+p)/2 | sin(72°) |
| cos(30°) | sqrt(3)/2 | sin(60°) |
| cos(36°) | p/2 | sin(54°) |
| cos(45°) | 1/sqrt(2) | sin(45°) |
| cos(54°) | sqrt(3-p)/2 | sin(36°) |
| cos(60°) | 1/2 | sin(30°) |
| cos(72°) | 1/(2p) | sin(18°) |

Central Angles of Planes |

Additional Angles |
However, as pointed out above, not all of the 120 Polyhedron's vertices are at the same radial distance from the center of volume. This means that not all of the vertices lie on the circumsphere. I am only illustrating the planes defined by these vertices and not the vertices themselves.