Consider now one of the regular Tetrahedra within the (yellow) FCC lattice.
The top triangle of this (blue) Tetrahedron is the same size as the triangular faces of the Octahedron Jitterbug (red).
The Jitterbug opens until these (red and blue) triangle faces match. (This was how we defined the size of the Jitterbug initially, above, so no surprise.)
Spinning the (blue) Tetrahedron defines another cone.
The cone angle is the same as the cone of equilibrium (force equal zero) between 2 Amperian current elements for the special case that the 2 current elements always point in the same direction.
The cone angle is exactly arccos(sqrt(2/3)) = 35.264389... degrees.
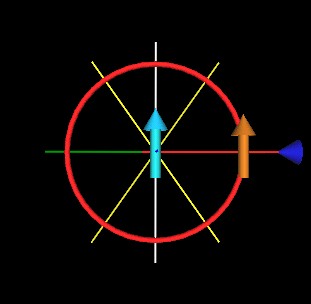
Consider the following figure showing 2 Amperian current elements.

In this case, when the 2 Amperian Current Elements (ACE) are side-by-side and pointing in the same direction, the orange/light brown ACE will experience an attractive force toward the light blue ACE, as indicated by the dark blue arrow/cone.
As the orange/light brown ACE is moved around the light blue ACE, along the red circle, there will be regoins for which the force will be repulsive (indicated by a red arrow/cone).
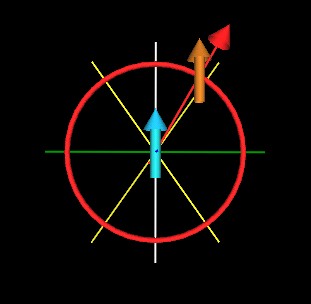
The light yellow lines indicates where the radial component of the force is zero, and divides the attractive force regions from the repulsive force regions. (Again, only the radial component of the complete force is being considered here. There are also torque forces on the 2 ACEs which are not considered here making this an artificial arrangement.)
Here is the complete force cycle for 2 Amperian current elements (which are constrained to point in the same direction).
Note that these 2 light yellow lines of zero radial force (equilibrium lines) make an angle of exactly arccos(sqrt(2/3)) = 35.264389... degrees with respect to the z-axis.
If we now rotate these light yellow equilibrium lines around the z-axis, we define 2 cones of equilibrium (cones of zero radial force).
This is the same cone as that generated by the blue regular Tetrahedron of the VE mentioned above (and, of course, of the Tetrahedra in the FCC lattice).
The equation for the radial component of the force between 2 Amperian current elements is given by
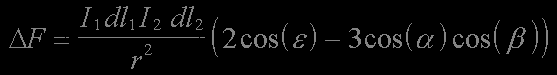
Note that this is refered to as "Ampere's force law" and should not be confused with "Ampere's Law" which is one of Maxwell's equations.
As before, epsilon is the angle between the 2 dipole's directions. For the case that the 2 dipoles are pointing in the same direction, epsilon=0°. Alpha and beta are the angles between the dipole direction and the line connecting the 2 dipoles together. In this case the 2 dipoles are pointing in the same direction so we have alpha=beta. The angular factor of the force equation is then
This factor is zero, and hence the radial force is zero, when
Which gives alpha = 35.264389...°, the same geometric cone angle mentioned above.
Here we have one Quantum Mechanical phenomenon (Angular Momentum Quantization) and two different classical electrodynamic phenomena:
Also note that
Usage Note: My work is copyrighted. You may use my work but you may not include my work, or parts of it, in any for-profit project without my consent.