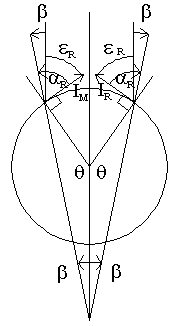
Consider a VACE (V_R) in the torus at some angle theta. There is a "mirror" VACE (V_L) on the left side of the torus.

What we are trying to prove is that the force F_L on the left current element I_L (due to the single external VACE) is equal to the negative of the force F_R on the right current element I_R.

This is easily seen from the following two illustrations.

In the first illustration we see the current element I_R on the right, tangent to the circle, at some angle theta. We construct the mirror of this current element about the right-left dividing line. This gives I_M. Note that angles alpha and epsilon are the same as defined by the right current element.

But this mirror current element I_M is pointing in the wrong direction. We want the current element on the left I_L to point 180 degrees from that of I_M.

I_L now defines the angles alpha_L and epsilon_L. In particular, we see that

This changes the angular factor in Ampere's force equation by an overall minus sign.

So, F_L = - F_R.

This means that for any force on the right that may be "pushing" on the torus, there is a corresponding force on the left which is "pulling" on the torus. The two torques are then additive and do not sum to zero (unless each torque is zero.)

Therefore, in determining the overall torque on the torus, we need only calculate the torque on the right hand side and then multiply by 2.

If the sum of all the torques on the right hand side do not sum to zero, as seems to be the case, then there is a net torque on the torus and it should rotate.

Usage Note: My work is copyrighted. You may use my work but you may not include my work, or parts of it, in any for-profit project without my consent.