

The tetrahelix is composed of face bonded tetrahedra.


See the web page here for more details on the Tetrahelix.
Recall that the Octhedron is obtainned by subdividing the edges and triangular faces of the Tetrahedron.
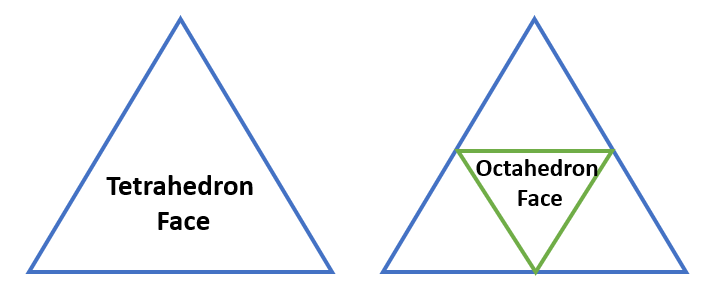
This means that there is an Octahelix within the Tetrahelix composed of face bonded Octahedra.
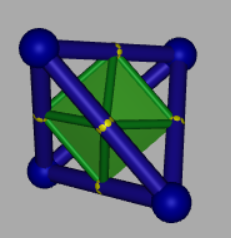


But the Icosahedron is obtainned by subdividing the triangular faces of the Octahedron.
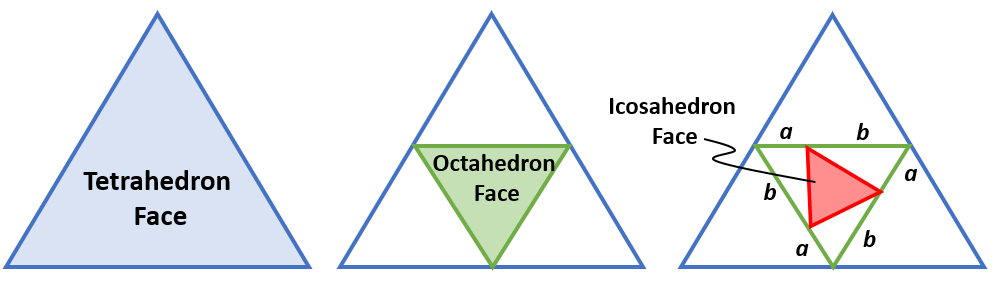
Each edge of the Octahedron is divided into segments of length "a" and "b". Let OEL be the Octahedron's Edge Length. Then b = OEL / phi, and a = OEL - b, where phi = (1 + sqrt(5))/2 is the Golden Ratio.
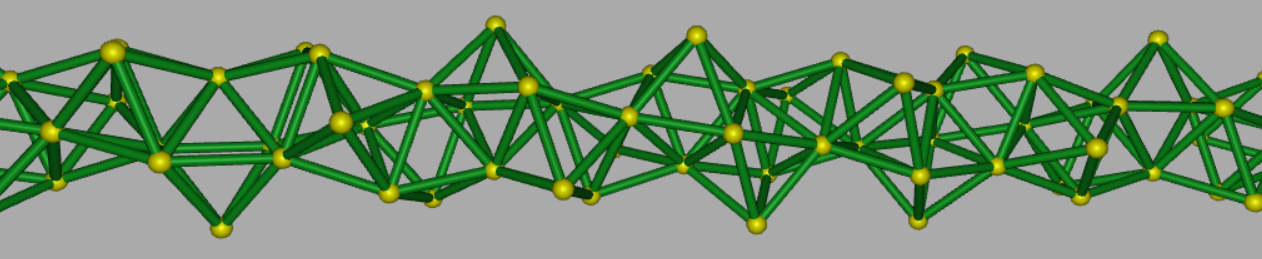
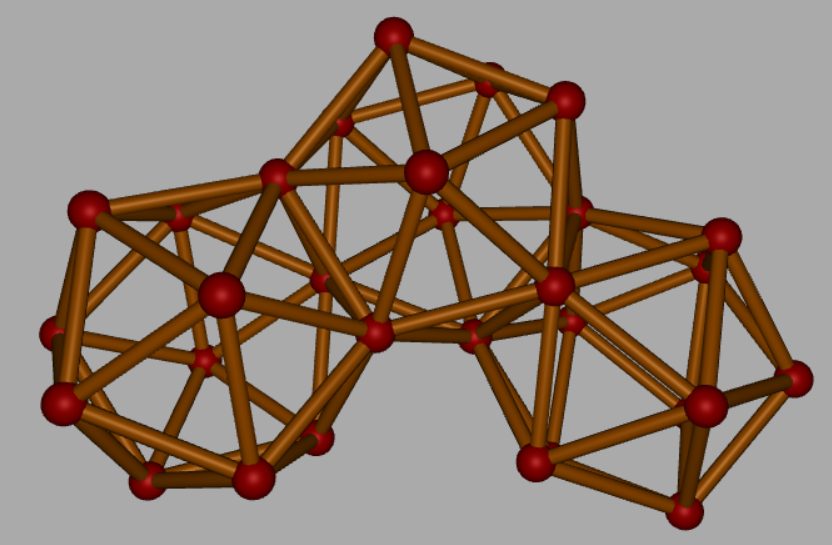
So, there is then an Icosahelix within the Octahelix within the Tetrahelix.




This shows how the Icosahedra are face bonded together...
Usage Note: My work is copyrighted. You may use my work but you may not include my work, or parts of it, in any for-profit project without my consent.