 '' is to be read as ``is defined to be''.
'' is to be read as ``is defined to be''.
I will briefly review some of the relations used in plane trigonometry. If you are not familiar with these relations you should consult an introductory text on plane trigonometry.
The symbol ``  '' is to be read as ``is defined to be''.
'' is to be read as ``is defined to be''.
Consider the right triangle shown in the figure. The angle ACB is
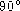 . Then
the edge lengths and the angles are related by (
. Then
the edge lengths and the angles are related by (  is the Greek letter
alpha)
is the Greek letter
alpha)
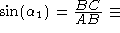 sine of the angle
sine of the angle 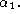
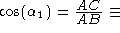 cosine of the angle
cosine of the angle 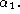
 tangent of the angle
tangent of the angle 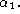
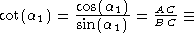 cotangent of the angle
cotangent of the angle 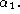

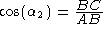



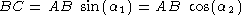
Because the triangle in the figure is a right triangle, the edges AC, BC, and AB obey Pythagoras' theorem.
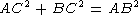
For any angle  (Greek letter beta),
(Greek letter beta), 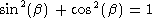 where
where 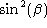 represents the second power of the sine function
and
represents the second power of the sine function
and 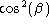 represents the second power of the cosine function. That
is
represents the second power of the cosine function. That
is 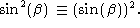
The inverse trigonometric functions are




The notation 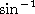 ,
,
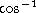 and
and
 does NOT mean the same
as in ordinary algebra. Whereas
does NOT mean the same
as in ordinary algebra. Whereas 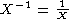 ,
, 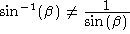 . This can lead to serious mistakes if you do not
realize that
. This can lead to serious mistakes if you do not
realize that  is just notation for the
is just notation for the  function.
function.
Angles are given in either units of radians or units of degrees. In the
following relation,  is in units of radians and
is in units of radians and 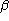 is in units
of degrees.
is in units
of degrees.

To convert from one system of units to the other, solve the above equation for
the unknown quantity. For example, if we know that  radians
and we want to know what this angle is in units of degrees, we solve for
radians
and we want to know what this angle is in units of degrees, we solve for
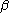 to get
to get
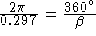
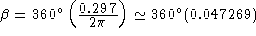
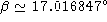
Note the use of the symbol `` '' which is read ``is approximately equal
to''. It is important to know when a given number is exact and when the number
is only an approximation. In Fuller's Synergetics books, Fuller does not
always make it clear when the numbers he is reporting are exact and when the
numbers are approximations. Therefore, you should be very careful when
repeating or using any of the numbers which you read from the Synergetics
books.
'' which is read ``is approximately equal
to''. It is important to know when a given number is exact and when the number
is only an approximation. In Fuller's Synergetics books, Fuller does not
always make it clear when the numbers he is reporting are exact and when the
numbers are approximations. Therefore, you should be very careful when
repeating or using any of the numbers which you read from the Synergetics
books.
It can be shown that the trigonometric functions obey the following relations:
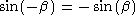
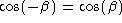
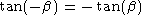
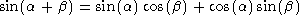
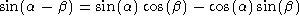
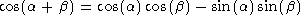
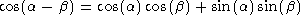
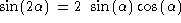
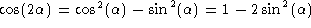
Of particular interest, note that
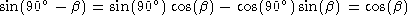

The angle 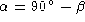 is called the complement of angle
is called the complement of angle
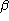 . The angle
. The angle 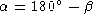 is called the supplement
of angle
is called the supplement
of angle  .
.
The following table has been taken from Tables Of Integrals And Other Mathematical Data, 4th edition, by H. B. Dwight, Macmillan Pub. Co., 1961.


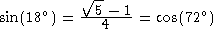
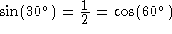

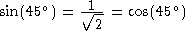
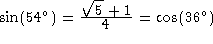
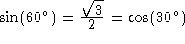
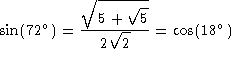
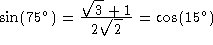
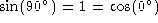
Usage Note: My work is copyrighted. You may use my work but
you may not include my work, or parts of it, in any
for-profit project
without my consent.