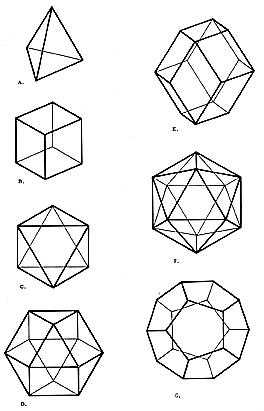
Fig. 400.30 Topological relationships of faces, vertexes,
and edges of various polyhedra:
| A. | Tetrahedron: 4 faces, 4 vertexes, 6 edges. |
| B. | Cube: 6 faces, 8 vertexes, 12 edges. |
| C. | Octahedron: 8 faces, 6 vertexes, 12 edges. |
| D. | Vector Equilibrium (cuboctahedron): 14 faces, 12
vertexes, 24 edges. |
| E. | Rhombic dodecahedron: 12 faces, 14 vertexes, 24 edges. |
| F. | Icosahedron: 20 faces, 12 vertexes 30 edges. |
| G. | Pentagonal dodecahedron: 12 faces, 20 vertexes, 30
edges. |
Euler's topological formula is f + (v - 2) = e, or f
+ v = e + 2. In any system, two vertexes may be
considered polarized. These vertexes are then subtracted
to balance the equation. This suggests the
inherent twoness of Universe.
|