453.00 Vector Equilibrium: Basic Equilibrium LCD Triangle

Fig. 453.01 		453.01 The system of 25 great circles of the vector equilibrium defines its own lowest common multiple spherical triangle, whose surface is exactly 1/48th of the entire sphere's surface. Within each of these l/4sth-sphere triangles and their boundary arcs are contained and repeated each time all of the unique interpatterning relationships of the 25 great circles. Twenty-four of the 48 triangles' patternings are "positive" and 24 are "negative," i.e., mirrorimages of one another, which condition is more accurately defined as "inside out" of one another. This inside-outing of the big triangles and each of their contained triangles is experimentally demonstrable by opening any triangle at any one of its vertexes and holding one of its edges while sweeping the other two in a 360-degree circling around the fixed edge to rejoin the triangle with its previous outsideness now inside of it. This is the basic equilibrium LCD triangle; for a discussion of the basic disequilibrium LCD triangle, see Sec. 905.

Fig. 453.02 		453.02 Inside-Outing of Triangle: The inside-outing transformation of a triangle is usually misidentified as "left vs. right," or "positive and negative," or as "existence vs. annihilation" in physics.
453.03 The inside-outing is four-dimensional and often complex. It functions as complex intro-extroverting.
454.00 Vector Equilibrium: Spherical Polyhedra Described by Great Circles

Fig. 454.01A

Fig. 454.01B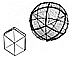

Fig. 454.01C 		454.01 The 25 great circles of the spherical vector equilibrium provide all the spherical edges for five spherical polyhedra: the tetrahedron, octahedron, cube, rhombic dodecahedron, and vector equilibrium, whose corresponding planar-faceted polyhedra are all volumetrically rational, even multiples of the tetrahedron. For instance, if the tetrahedron's volume is taken as unity, the octahedron's volume is four, the cube's volume is three, the rhombic dodecahedron's is six, and the vector cquilibrium's is 20 (see drawings section).
454.02 This is the hierarchy of rational energy quanta values in synergetics, which the author discovered in his youth when he first sought for an omnirational coordinate system of Universe in equilibrium against which to measure the relative degrees of orderly asymmetries consequent to the cosmic myriad of pulsatively propagated energetic transactions and transformations of eternally conserving evolutionary events. Though almost all the involved geometries were long well known, they had always been quantized in terms of the cube as volumetric unity and its edges as linear unity; when employed in evaluating the other polyhedra, this method produced such a disarray of irrational fraction values as to imply that the other polyhedra were only side-show geometric freaks or, at best, "interesting aesthetic objets d'art." That secondpowering exists today in academic brains only as "squaring" and thirdpowering only as cubing is manifest in any scientific blackboard discourse, as the scientists always speak of the x2 they have just used as "x squared" and likewise always account x3 as "x cubed" (see drawings section).
454.03 The spherical tetrahedron is composed of four spherical triangles, each consisting of 12 basic, least-common-denominator spherical triangles of vector equilibrium.
454.04 The spherical octahedron is composed of eight spherical triangles, each consisting of six basic-vector-equilibrium, least-common-denominator triangles of the 25 great-circle, spherical-grid triangles.
454.05 The spherical cube is composed of six spherical squares with corners of 120 each, each consisting of eight basic-vector-equilibrium, leastcommon-denominator triangles of the 25 great-circle spherical-grid triangles.

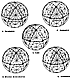Fig. 454.06 		454.06 The spherical rhombic dodecahedron is composed of 12 spherical diamond- rhombic faces, each composed of four basic-vector-equilibrium, least-common- denominator triangles of the 25 great-circle, spherical-grid triangles.
455.00 Great-Circle Foldabilities of Vector Equilibrium
455.01 Foldability of Vector Equilibrium Four Great-Circle Bow Ties: All of the set of four great circles uniquely and discretely describing the vector equilibrium can be folded out of four whole (non-incised), uniformradius, circular discs of paper, each folded radially in 60-degree central angle increments, with two diametric folds, mid-circle, hinge-bent together and locked in radial congruence so that their six 60-degree arc edges form two equiangled spherical triangles, with one common radius-pairing fastened together at its external apex, that look like a bow tie. The pattern corresponds to the external arc trigonometry, with every third edgefold being brought into congruence to form great-circle-triangled openings at their top with their pointed lower ends all converging ice-cream-cone-like at the center of the whole uncut and only radially folded great circles. When the four bow ties produced by the folded circles are assembled together by radii congruence and locking of each of their four outer bow-tie corners to the outer bow-tie corners of one another, they will reestablish the original four great-circle edge lines of the vector equilibrium and will accurately define both its surface arcs and its central angles as well as locating the vector-equilibrium axes of symmetry of its three subsets of great-circle-arc-generating to produce, all told, 25 great circles of symmetry. When assembled with their counterpart foldings of a total number corresponding to the great-circle set involved, they will produce a whole sphere in which all of the original great circles are apparently restored to their completely continuing-around-the-sphere integrity.
455.02 The sum of the areas of the four great-circle discs elegantly equals the surface area of the sphere they define. The area of one circle is r2. The area of the surface of a sphere is 4r2. The area of the combined four folded great-circle planes is also 4r2 and all four great-circle planes go through the exact center of the sphere and, between them, contain no volume at all. The sphere contains the most volume with the least surface enclosure of any geometrical form. This is a cosmic limit at maximum. Here we witness the same surface with no volume at all, which qualifies the vector equilibrium as the most economic nuclear "nothingness" whose coordinate conceptuality rationally accommodates all radiational and gravitational interperturbational transformation accounting. In the four great-circle planes we witness the same surface area as that of the sphere, but containing no volume at all. This too, is cosmic limit at zero minimumness.
455.03 It is to be noted that the four great-circle planes of the vector equilibrium passing exactly through its and one another's exact centers are parallel to the four planes of the eight tetrahedra, which they accommodate in the eight triangular bow-tie concavities of the vector equilibrium. The four planes of the tetrahedra have closed on one another to produce a tetrahedron of no volume and no size at all congruent with the sizeless center of the sphere defined by the vector equilibrium and its four hexagonally intersected planes. As four points are the minimum necessary to define the insideness and outsideness unique to all systems, four triangular facets are the minimum required to define and isolate a system from the rest of Universe.
455.04 Four is also the minimum number of great circles that may be folded into local bow ties and fastened corner-to-corner to make the whole sphere again and reestablish all the great circles without having any surfaces double or be congruent with others or without cutting into any of the circles.
455.05 These four great-circle sets of the vector equilibrium demonstrate all the shortest, most economical railroad "routes" between all the points in Universe, traveling either convexly or concavely. The physical-energy travel patterns can either follow the great-circle routes from sphere to sphere or go around in local holding patterns of figure eights on one sphere. Either is permitted and accommodated. The four great circles each go through six interspherical tangency points.
455.10 Foldability of Vector Equilibrium Six Great-Circle Bow Ties: The foldable bow ties of the six great circles of the vector equilibrium define a combination of the positive and negative spherical tetrahedrons within the spherical cube as well as of the rhombic dodecahedron.

Fig. 455.11 		455.11 In the vector equilibrium's six great-circle bow ties, all the internal, i.e., central angles of 70° 32' and 54° 44', are those of the surface angles of the vector equilibrium's four great-circle bow ties, and vice versa. This phenomenon of turning the inside central angles outwardly and the outside surface angles inwardly, with various fractionations and additions, characterizes the progressive transformations of the vector equilibrium from one greatcircle foldable group into another, into its successive stages of the spherical cube and octahedron with all of their central and surface angles being both 90 degrees even.

Fig. 455.20 		455.20 Foldability of 12 Great Circles into Vector Equilibrium: We can take a disc of paper, which is inherently of 360 degrees, and having calculated with spherical trigonometry all the surface and central angles of both the associated and separate groups of 3__ 4__ 6__ 12 great circles of the vector equilibrium's 25 great circles, we can lay out the spherical arcs which always subtend the central angles. The 25 great circles interfere with and in effect "bounce off" or penetrate one another in an omnitriangulated, nonredundant spherical triangle grid. Knowing the central angles, we can lay them out and describe foldable triangles in such a way that they make a plurality of tetrahedra that permit and accommodate fastening together edge-to-edge with no edge duplication or overlap. When each set, 312, of the vector equilibrium is completed, its components may be associated with one another to produce complete spheres with their respective great- circle, 360-degree integrity reestablished by their arc increment association.
455.21 The 25 folded great-circle sections join togetha to reestablish the 25 great circles. In doing so, they provide a plurality of 360-degree local and long-distance travel routes. Because each folded great circle starts off with a 360-degree disc, it maintains that 360-degree integrity when folded into the bow-tie complexes. It is characteristic of electromagnetic wave phenomena that a wave must retum upon itself, completing a 360- degree circuit. The great-circle discs folded or flat provide unitary-wave-cycle circumferential circuits. Therefore, folded or not, they act like waves coming back upon themselves in a perfect wave control. We find their precessional cyclic sdf-interferences producing angular resultants that shunt themselves into little local 360-degree, bow-tie "holding patterns." The entire behavior is characteristic of generalized wave phenomena.
455.22 In the case of the 12 great circles of the vector equilibrium, various complex transformative, anticipatory accommodations are manifest, such as that of the 12 sets of two half-size pentagons appearing in the last, most complex great-circle set of the vector equilibrium, which anticipates the formation of 12 whole pentagons in the six great-circle set of the 31 great circles of the icosahedron into which the vector equilibrium first transforms contractively.
Next Section: 456.00
Copyright © 1997 Estate of R. Buckminster Fuller