Polyhedra Dynamics

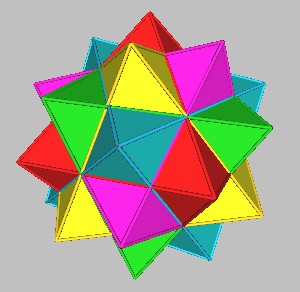
5 Cubes in the Dodecahedron.

From the rotation of 4 Cubes + 1 fixed Cube?

The 4 rotation axes used are the 4 vertex-to-opposite-vertex axes.

For each Cube there is a complementary ("dual") polyhedron: the Octahedron.

Look at the rotation of 4 Octahedra + 1 fixed Octahedron.
Using the same 4 rotation axes, which for the Octahedron,
are the 4 face-center-to-opposite-face-center axes.

This produces a "120 polyhedron" having 120 faces.

Assemble the 5 cubes (10 Tetrahedra) and 5 rhombic Dodecahedra
and the Icosahedron, Dodecahedron and the rhombic Triacontahedron
we get another 120 polyhedron.

This is the polyhedron that Lynnclaire Dennis and I have been exploring.

3 different views of stick model.

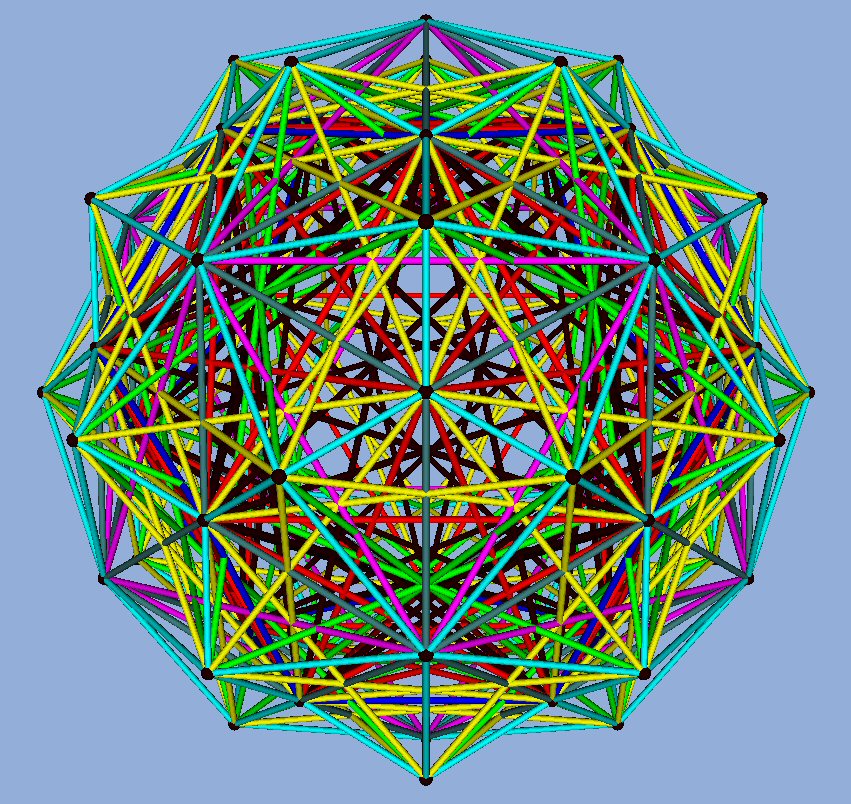
Another 120 (spherical) polyhedron is well known to be generated
by the (12 + 20 + 30)/2 = 31 axes of symmetry of the Icosahedron.