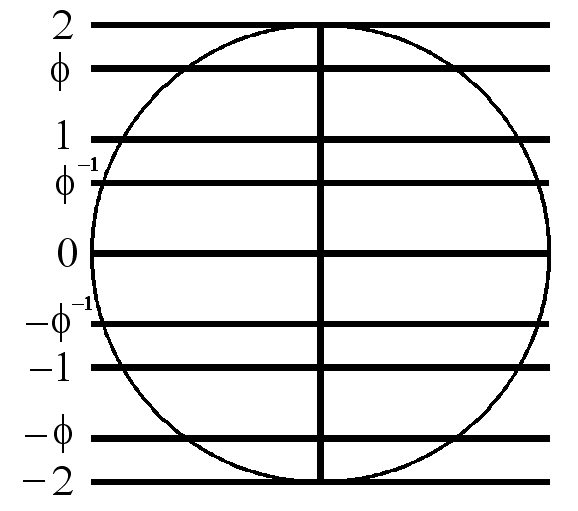
The (x, y, z) coordinates for all of the vertices
can be put into the form
n φm
where n = -2, -1, 0, 1, 2 and m = -1, 0, 1 and φ is the Golden ratio.
|
|
|
φ = (1 + √5) / 2 = 1.618033989...
φ-1 = φ - 1 = 0.618033989...
| Type "A" = | Octahedron vertex |
| Type "B" = | Icosahedron vertex |
| Type "C" = | Tetrahedron, Cube, Dodecahedron vertex |
Note the z-components are 2, φ, 1, φ-1, 0,
-φ-1, -1, -φ, -2.
This defines 9 layers or planes (in this orientation of the 120 Polyhedron).

The Cube's 4 vertex-to-opposite-vertex axes were used
for the Cube and Octahedron's rotations.
What are the rotation angles?
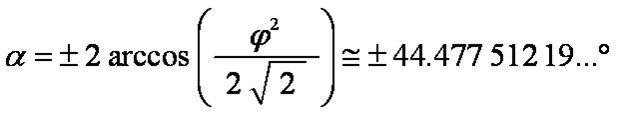
|
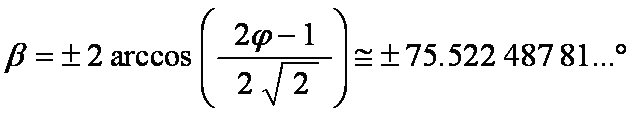
|
|α| + |β| = 120°
For an arbitrary (x, y, z) coordinate, if rotated by these angles
what is the resulting coordinate (x', y', z')?
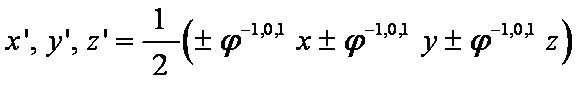
Copyright September, 2007 by Robert W. Gray