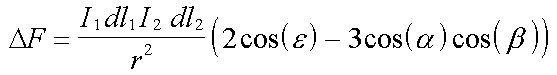
Ampere developed an equation for the force between 2 current elements.

Ampere's equation can be written as

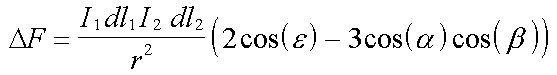
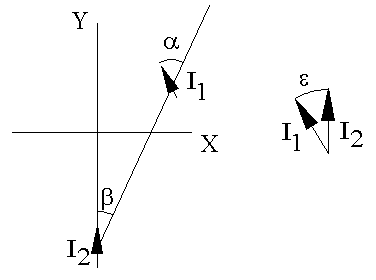
Epsilon is the angle through which current element #2 has to be rotated to point in the same direction as current element #1. Consider the line drawn from current element #2 through current element #1. Then the angle alpha is the angle through which current element #1 must be rotated to point along this line. And beta is the angle though which current element #2 must be rotated to point along this line.

The first thing to point out is that an "Ampere current element" is not the same thing as the "electron flow current" you learned about in physics or electrical engineering classes. For a discussion of this see the books Newtonian Electrodynamics by Peter Graneau and Neal Graneau, World Scientific, 1996 and Ampere-Neumann Electrodynamics of Metals, 2nd edition by Peter Graneau, Hadronic Press, 1994.

It has been suggested that an Ampere current element may be realized by circularly magnetizing a torus or a flat ring ("washer") shaped magnet so that all of the magnetic "field lines" are internal to the magnetic material. These magnets have been called VACEs. VACE stands for Virtual Ampere Current Element.

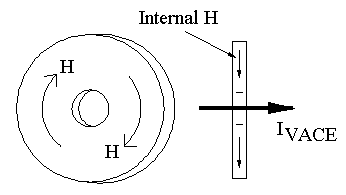
If this does indeed give a realization to Ampere current elements then it might be possible to realize a non-magnetic magnet motor which requires no electrical input to run. By "non-magnetic" I mean that the magnetic fields are not "used", but the magnet as a whole, properly magnetized, is used. So, we would have a non-magnetic magnet motor.

For example, arrange the washer VACE magnets in a circle to form a torus. This results in the Ampere current elements aligned along a circle.

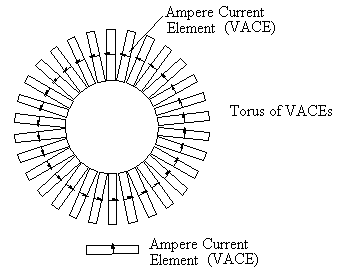
Next, place another VACE external to the torus of VACEs such that it is pointing toward the center of the torus. The current elements making up the torus and the external current element are all in the same plain.

Question: What is the net torque on the torus of VACEs about the torus symmetry axes?

Using Ampere's force equation, we can calculate the force on each of the current elements. We find that there is a net torque on the torus about its symmetry axes. So the torus should self-rotate.

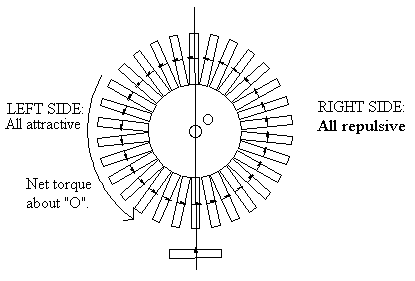
To see this, we calculate the magnitude of the Ampere force on each of the VACEs in the torus due to the single external VACE. The following diagram gives the results.

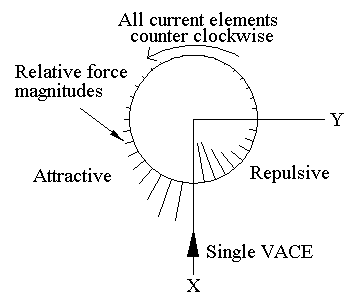
In the above diagram, the circle represents the collection of VACEs which form the torus. At each VACE location there is a "force magnitude" drawn. These lines do not indicate the direction of the force. They only represent the relative magnitude of the force. Those lines which are drawn inside the circle represent repulsive forces away from the single external VACE. Those lines drawn outside the circle represent attractive forces toward the external VACE. The direction of each force is along the line joining the external VACE and the VACE in the torus for which the force is being calculated.

Lets do a little "sanity check" by carrying out the calculation for 3 of the VACEs in the torus as shown below.

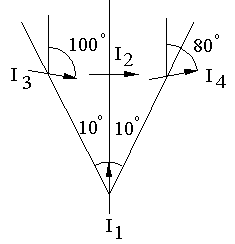
We are really only interested in the angular part of Ampere's force equation.

For I1 and I2, beta = 0, alpha = 90 degrees and epsilon = 90 degrees. So, cos(epsilon) = 0 and cos(alpha) = 0 which means the force is zero.

Next consider I1 and I3 for which beta = 10 degrees, alpha = 110 degrees, and epsilon = 100 degrees. Then cos(epsilon) = -0.1736, cos(alpha) = -0.3420, and cos(beta) = 0.9848. The angular part of Ampere's force equation is then

Finally consider I1 and I4 for which beta = 10 degrees, alpha = 70 degrees, and epsilon = 80 degrees. Then cos(epsilon) = 0.1736, cos(alpha) = 0.3420, and cos(beta) = 0.9848. The angular part of Ampere's force equation is then

So, we have explicitly calculated that a VACE "a little to the left" of the external VACE will experience an attractive force while a VACE "a little to the right" will experience a repulsive force. This is what "causes" the torus of VACEs to self-rotate.

If this is truely the case, then there is no reason to have just 1 external VACE. We can position many VACEs all around the torus, as shown below.

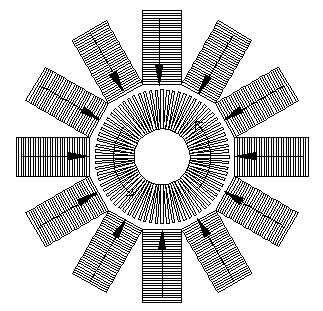
This, of course. makes no sense from an energy point of view.

In the idealization in which the Ampere current elements form a continuous circle, there is no difference in energy for any angle of rotation about the symmetry axis "O" of the torus. So, there should be no net torque on the torus about "O". (Forces and torques only arise if there is an energy difference between orientations or positions.) But Ampere's force equation seems to indicate a net torque. So, if the energy symmetry argument is correct, where is the counter force (and torque) coming from?

If you can find a problem with this analysis, please let me know. I don't need to be "promoting" ideas known to be wrong.

Here are more details on the torque calculations.

Here is an interactive program you can use to calculate the net "relative" torque on the VACE torus.

Usage Note: My work is copyrighted. You may use my work but you may not include my work, or parts of it, in any for-profit project without my consent.