
 Principle of Angular Topology
Principle of Angular Topology

|
224.00  Principle of Angular Topology
Principle of Angular Topology
|

|
224.01
 Definition: When expressed in terms of cyclic unity
the sum of the angles
around all the vertexes of a structural system, plus
720 degrees, equals the number of
vertexes of the system multiplied by 360 degrees.
Definition: When expressed in terms of cyclic unity
the sum of the angles
around all the vertexes of a structural system, plus
720 degrees, equals the number of
vertexes of the system multiplied by 360 degrees.
|

|
224.02
 All local structural systems in Universe are always
accomplished by nature
through the elimination of 720 degrees of angle. This
is the way in which nature takes two
complete 360-degree angular tucks in the illusory infinity
of a plane to render systems
locally and visibly finite. The difference between visually
finite systems and illusory infinity
is two cyclic unities.
All local structural systems in Universe are always
accomplished by nature
through the elimination of 720 degrees of angle. This
is the way in which nature takes two
complete 360-degree angular tucks in the illusory infinity
of a plane to render systems
locally and visibly finite. The difference between visually
finite systems and illusory infinity
is two cyclic unities.
|

|
224.03
 Structural systems are local, closed, and finite.
They include all geometric
forms, symmetric or asymmetric, simple or complex. Structural
systems can have only one
inside and only one outside. Two or more structures
may be concentric and triangularly
interconnected to operate as one structure.
Structural systems are local, closed, and finite.
They include all geometric
forms, symmetric or asymmetric, simple or complex. Structural
systems can have only one
inside and only one outside. Two or more structures
may be concentric and triangularly
interconnected to operate as one structure.
|

|
224.04
 The difference between the sum of all the angles around
all the vertexes of
any system and the total number of vertexes times 360º
(as angular unity) is 720º, which
equals two unities. The sum of the angles of a tetrahedron
always equals 720º. The
tetrahedron may be identified as the 720 differential
between any definite local
geometrical system (such as Greek "solid" geometry)
and finite universe.
The difference between the sum of all the angles around
all the vertexes of
any system and the total number of vertexes times 360º
(as angular unity) is 720º, which
equals two unities. The sum of the angles of a tetrahedron
always equals 720º. The
tetrahedron may be identified as the 720 differential
between any definite local
geometrical system (such as Greek "solid" geometry)
and finite universe.
|

|
224.05
 Line: A line has two vertexes with angles around each
of its vertexial ends
equal to 0º. The sum of these angles is 0º . The sum
of the vertexes (two) times angular
unity (360º ) is 720º.
The remainder of 0º from 720º is
720º, or two unities, or one
tetrahedron. Q.E.D.
Line: A line has two vertexes with angles around each
of its vertexial ends
equal to 0º. The sum of these angles is 0º . The sum
of the vertexes (two) times angular
unity (360º ) is 720º.
The remainder of 0º from 720º is
720º, or two unities, or one
tetrahedron. Q.E.D.
|

|
224.06
 Triangle: The three angles of one “face” of a planar
triangle always add up
to 180º as a phenomenon independent of the relative dimensional
size of the triangles.
One-half of definitive cyclic unity is 180º. Every triangle
has two faces__its obverse and
reverse. Unity is two. So we note that the angles of
both faces of a triangle add up to
360º. Externally, the sum of the angles around each
of the triangle’s three vertexes is
120º, of which 60º is on the obverse side of each vertex;
for a triangle, like a line, if it
exists, is an isolatable system always having positive
and negative aspects. So the sum of
the vertexes around a triangle (three) times 360º equals
1080º. The remainder of 360º
from 1080º leaves 720º, or one tetrahedron. Q.E.D.
Triangle: The three angles of one “face” of a planar
triangle always add up
to 180º as a phenomenon independent of the relative dimensional
size of the triangles.
One-half of definitive cyclic unity is 180º. Every triangle
has two faces__its obverse and
reverse. Unity is two. So we note that the angles of
both faces of a triangle add up to
360º. Externally, the sum of the angles around each
of the triangle’s three vertexes is
120º, of which 60º is on the obverse side of each vertex;
for a triangle, like a line, if it
exists, is an isolatable system always having positive
and negative aspects. So the sum of
the vertexes around a triangle (three) times 360º equals
1080º. The remainder of 360º
from 1080º leaves 720º, or one tetrahedron. Q.E.D.
|

|
224.07
 Sphere: The Greeks defined the sphere as a surface
outwardly equidistant in
all directions from a point. As defined, the Greeks’
sphere's surface was an absolute
continuum, subdividing all the Universe outside it from
all the Universe inside it;
wherefore, the Universe outside could be dispensed with
and the interior eternally
conserved. We find local spherical systems of Universe
are definite rather than infinite as
presupposed by the calculus's erroneous assumption of
360-degreeness of surface plane
azimuth around every point on a sphere. All spheres
consist of a high-frequency
constellation of event points, all of which are approximately
equidistant from one central
event point. All the points in the surface of a sphere
may be interconnected. Most
economically interconnected, they will subdivide the
surface of the sphere into an
omnitriangulated spherical web matrix. As the frequency
of triangular subdivisions of a
spherical constellation of omnitriangulated points approaches
subvisibility, the difference
between the sums of the angles around all the vertex
points and the numbers of vertexes,
multiplied by 360 degrees, remains constantly
720 degrees,
which is the sum of the angles
of two times unity (of 360 degrees), which equals one
tetrahedron. Q.E.D.
Sphere: The Greeks defined the sphere as a surface
outwardly equidistant in
all directions from a point. As defined, the Greeks’
sphere's surface was an absolute
continuum, subdividing all the Universe outside it from
all the Universe inside it;
wherefore, the Universe outside could be dispensed with
and the interior eternally
conserved. We find local spherical systems of Universe
are definite rather than infinite as
presupposed by the calculus's erroneous assumption of
360-degreeness of surface plane
azimuth around every point on a sphere. All spheres
consist of a high-frequency
constellation of event points, all of which are approximately
equidistant from one central
event point. All the points in the surface of a sphere
may be interconnected. Most
economically interconnected, they will subdivide the
surface of the sphere into an
omnitriangulated spherical web matrix. As the frequency
of triangular subdivisions of a
spherical constellation of omnitriangulated points approaches
subvisibility, the difference
between the sums of the angles around all the vertex
points and the numbers of vertexes,
multiplied by 360 degrees, remains constantly
720 degrees,
which is the sum of the angles
of two times unity (of 360 degrees), which equals one
tetrahedron. Q.E.D.
|

|
224.08
 Tetrahedron: The sum of the angles of a tetrahedron,
regular or irregular, is
always 720º, just as the sum of the angles of a planar
triangle is always 180º. Thus, we
may state two propositions as follows:
Tetrahedron: The sum of the angles of a tetrahedron,
regular or irregular, is
always 720º, just as the sum of the angles of a planar
triangle is always 180º. Thus, we
may state two propositions as follows:
|

|
224.081
 The sum of the surface angles of any polyhedron equals
the number of
vertexes multiplied by 360º minus one tetrahedron; and
The sum of the surface angles of any polyhedron equals
the number of
vertexes multiplied by 360º minus one tetrahedron; and
|

|
224.082
 The sum of the angles of any polyhedron (including
a sphere) is always
evenly divisible by one tetrahedron.
The sum of the angles of any polyhedron (including
a sphere) is always
evenly divisible by one tetrahedron.
|

|
224.10
 Descartes: Descartes is the first of record to have
discovered that the sum of
the angles of a polyhedron is always 720º less than the
number of vertexes times 360º.
Descartes did not equate the 720º with the tetrahedron
or with the one unit of energy
quantum that it vectorially constitutes. He did not
recognize the constant, whole difference
between the visibly definite system and the invisibly
finite Universe, which is always
exactly one finite invisible tetrahedron outwardly and
one finite invisible tetrahedron
inwardly.
Descartes: Descartes is the first of record to have
discovered that the sum of
the angles of a polyhedron is always 720º less than the
number of vertexes times 360º.
Descartes did not equate the 720º with the tetrahedron
or with the one unit of energy
quantum that it vectorially constitutes. He did not
recognize the constant, whole difference
between the visibly definite system and the invisibly
finite Universe, which is always
exactly one finite invisible tetrahedron outwardly and
one finite invisible tetrahedron
inwardly.
|

|
224.11
 The Calculus: The calculus assumes that a sphere is
infinitesimally
congruent with a sphere to which it is tangent. The
calculus and spherical trigonometry
alike assume that the sum of the angles around any point
on any sphere’s surface is always
360 degrees. Because spheres are not continuous surfaces
but are polyhedra defined by
the vectorially interconnecting chords of an astronomical
number of event foci (points)
approximately equidistant from one approximate point,
these spherically appearing
polyhedra__whose chords emerge from lesser radius midpoints
to maximum radius
convergences at each of the spherically appearing polyhedra's
vertexes, ergo, to convex
external joining__must follow the law of polyhedra by
which the sum of all the angles
around the vertexes of the polyhedra is always 720 degrees
less than 360 degrees times the
number of vertexes. The demonstration thus far made
discloses that the sum of the angles
around all the vertexes of a sphere will always be 720
degrees or one tetrahedron__less
than the sum of the vertexes times 360 degrees__ergo,
one basic assumption of the
calculus and spherical trigonometry is invalid.
The Calculus: The calculus assumes that a sphere is
infinitesimally
congruent with a sphere to which it is tangent. The
calculus and spherical trigonometry
alike assume that the sum of the angles around any point
on any sphere’s surface is always
360 degrees. Because spheres are not continuous surfaces
but are polyhedra defined by
the vectorially interconnecting chords of an astronomical
number of event foci (points)
approximately equidistant from one approximate point,
these spherically appearing
polyhedra__whose chords emerge from lesser radius midpoints
to maximum radius
convergences at each of the spherically appearing polyhedra's
vertexes, ergo, to convex
external joining__must follow the law of polyhedra by
which the sum of all the angles
around the vertexes of the polyhedra is always 720 degrees
less than 360 degrees times the
number of vertexes. The demonstration thus far made
discloses that the sum of the angles
around all the vertexes of a sphere will always be 720
degrees or one tetrahedron__less
than the sum of the vertexes times 360 degrees__ergo,
one basic assumption of the
calculus and spherical trigonometry is invalid.
|

|
224.12
 Cyclic Unity: We may also say that: where unity (1)
equals 360º , 180º
equals one-half unity (1/2), and that 720º equals two
times unity (2); therefore, we may
identify a triangle as one-half unity and a tetrahedron
as cyclic unity of two. As the sum of
a polyhedron’s angles, 720º is unique to the tetrahedron;
720º is the angular name of the
tetrahedron. 720º is two cyclic unities. The tetrahedron
is the geometrical manifest of
“unity is plural and, at minimum, is two.” The tetrahedron
is twoness because it is
congruently both a concave tetrahedron and a convex
tetrahedron.
Cyclic Unity: We may also say that: where unity (1)
equals 360º , 180º
equals one-half unity (1/2), and that 720º equals two
times unity (2); therefore, we may
identify a triangle as one-half unity and a tetrahedron
as cyclic unity of two. As the sum of
a polyhedron’s angles, 720º is unique to the tetrahedron;
720º is the angular name of the
tetrahedron. 720º is two cyclic unities. The tetrahedron
is the geometrical manifest of
“unity is plural and, at minimum, is two.” The tetrahedron
is twoness because it is
congruently both a concave tetrahedron and a convex
tetrahedron.
|

|
224.13
 Where cyclic unity is taken as 360 degrees of central
angle, the difference
between infinity and finity is always exactly two, or
720 degrees, or two times 360
degrees, or two times unity. Cyclic unity embraces both
wave and frequency since it
represents angles as well as cycles. This is topologically
manifest in that the number of
vertexes in any structural system multiplied by 360
degrees, minus two times 360 degrees,
equals the sum of the angles around all the vertexes
of the system.
Where cyclic unity is taken as 360 degrees of central
angle, the difference
between infinity and finity is always exactly two, or
720 degrees, or two times 360
degrees, or two times unity. Cyclic unity embraces both
wave and frequency since it
represents angles as well as cycles. This is topologically
manifest in that the number of
vertexes in any structural system multiplied by 360
degrees, minus two times 360 degrees,
equals the sum of the angles around all the vertexes
of the system.
|
 Table 224.20 |
224.20
 Equation of Angular Topology:
Equation of Angular Topology:
|

|
224.30
 Polarity: Absolutely straight lines or an absolutely
flat plane would
theoretically continue outward to infinity. The difference
between infinity and finity is
governed by the taking out of angular sinuses, like
pieces of pie, out of surface areas
around a point in an absolute plane. This is the way
lampshades and skirts are made.
Joining the sinused fan-ends together makes a cone;
if two cones are made and their open
(ergo, infinitely trending) edges are brought together,
a finite system results. It has two
polar points and an equator. These are inherent and
primary characteristics of all systems.
Polarity: Absolutely straight lines or an absolutely
flat plane would
theoretically continue outward to infinity. The difference
between infinity and finity is
governed by the taking out of angular sinuses, like
pieces of pie, out of surface areas
around a point in an absolute plane. This is the way
lampshades and skirts are made.
Joining the sinused fan-ends together makes a cone;
if two cones are made and their open
(ergo, infinitely trending) edges are brought together,
a finite system results. It has two
polar points and an equator. These are inherent and
primary characteristics of all systems.
|

|
224.40
 Multivalent Applications: Multiple-bonded bivalent
and trivalent
tetrahedral and octahedral systems follow the law of
angular topology. Single-bonded
monovalent tetrahedral and octahedral arrangements do
not constitute a system; they are
half systems, and in their case the equation would be:
Multivalent Applications: Multiple-bonded bivalent
and trivalent
tetrahedral and octahedral systems follow the law of
angular topology. Single-bonded
monovalent tetrahedral and octahedral arrangements do
not constitute a system; they are
half systems, and in their case the equation would be:
|

|
224.50
 Corollary: Principle of Finite Universe Conservation:
By our systematic
accounting of angularly definable convex-concave local
systems, we discover that the sum
of the angles around each of every local system's interrelated
vertexes is always two cyclic
unities less than universal nondefined finite totality.
We call this discovery the principle of
finite Universe conservation. Therefore, mathematically
speaking, all defined
conceptioning always equals finite Universe minus two.
The indefinable quality of finite
Universe inscrutability is exactly accountable as two.
Corollary: Principle of Finite Universe Conservation:
By our systematic
accounting of angularly definable convex-concave local
systems, we discover that the sum
of the angles around each of every local system's interrelated
vertexes is always two cyclic
unities less than universal nondefined finite totality.
We call this discovery the principle of
finite Universe conservation. Therefore, mathematically
speaking, all defined
conceptioning always equals finite Universe minus two.
The indefinable quality of finite
Universe inscrutability is exactly accountable as two.
|

|
224.60
 Tetrahedral Mensuration: The sum of the angles around
all vertexes of
any polyhedral system is evenly divisible by the sum
of the angles of a tetrahedron. The
volumes of all systems may be expressed in tetrahedra.
Tetrahedral Mensuration: The sum of the angles around
all vertexes of
any polyhedral system is evenly divisible by the sum
of the angles of a tetrahedron. The
volumes of all systems may be expressed in tetrahedra.
|
 Table 224.70A |
224.70
 Equation of Tetrahedral Mensuration:
Equation of Tetrahedral Mensuration:
|
||||
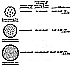 Table 224.70B |

|
225.00
 Principle of Design Covariables
Principle of Design Covariables
|

|
225.01
 Definition: The principle of design covariables states
that angle and
frequency modulation, either subjective or objective
in respect to man's consciousness,
discretely defines all events or experiences which altogether
constitute Universe.
Definition: The principle of design covariables states
that angle and
frequency modulation, either subjective or objective
in respect to man's consciousness,
discretely defines all events or experiences which altogether
constitute Universe.
|

|
225.02
 There are only two possible covariables operative
in all design in the
Universe. They are modifications of angle and frequency.
There are only two possible covariables operative
in all design in the
Universe. They are modifications of angle and frequency.
|

|
225.03
 Local structure is a set of frequency associable (spontaneously
tunable),
recollectible experience relationships, having a regenerative
constellar patterning as the
precessional resultants of concentrically shunted, periodic
self-interferences, or
coincidences of its systematic plurality of definitive
vectorial frequency wavelength and
angle interrelationships.
Local structure is a set of frequency associable (spontaneously
tunable),
recollectible experience relationships, having a regenerative
constellar patterning as the
precessional resultants of concentrically shunted, periodic
self-interferences, or
coincidences of its systematic plurality of definitive
vectorial frequency wavelength and
angle interrelationships.
|

|
226.00
 Principle of Functions
Principle of Functions
|

|
226.01
 Definition: The principle of functions states that
a function can always and
only coexist with another function as demonstrated experimentally
in all systems as the
outside-inside, convex-concave, clockwise-counterclockwise,
tension-compression
couples.
Definition: The principle of functions states that
a function can always and
only coexist with another function as demonstrated experimentally
in all systems as the
outside-inside, convex-concave, clockwise-counterclockwise,
tension-compression
couples.
|

|
226.02
 Functions occur only as inherently cooperative and
accommodatively varying
subaspects of synergetically transforming wholes.
Functions occur only as inherently cooperative and
accommodatively varying
subaspects of synergetically transforming wholes.
|

|
226.10
 Corollary: Principle of Complementarity: A corollary
of the principle of
functions is the principle of complementarity, which
states that two descriptions or sets of
concepts, though mutually exclusive, are nevertheless
both necessary for an exhaustive
description of the situation.
Corollary: Principle of Complementarity: A corollary
of the principle of
functions is the principle of complementarity, which
states that two descriptions or sets of
concepts, though mutually exclusive, are nevertheless
both necessary for an exhaustive
description of the situation.
|

|
226.11
 Every fundamental behavior patterning in Universe
always and only coexists
with a complementary but non-mirror-imaged patterning.
Every fundamental behavior patterning in Universe
always and only coexists
with a complementary but non-mirror-imaged patterning.
|

|
227.00 Principle of Order Underlying Randomness |
 Table 227.01 |
227.01
 Definition: The number of relationships between events
is always
Definition: The number of relationships between events
is always
|

|
227.02
 The relationships between four or more events are
always greater in number
than the number of events. The equation expresses the
conceptuality of the number of the
most economical relationships between events or the
minimum number of interconnections
of all events.
The relationships between four or more events are
always greater in number
than the number of events. The equation expresses the
conceptuality of the number of the
most economical relationships between events or the
minimum number of interconnections
of all events.
|

|
227.03
 The number of telephone lines necessary to interequip
various numbers of
individuals so that any two individuals will always
have their unique private telephone line
is always (N 2 - N)/2, where N
is the number of telephones.
This is to say that all the
special interrelationships of all experiences define
comprehension, which is the number of
connections necessary to an understanding of "what everything
is all about." When we
understand, we have all the fundamental connections
between the star events of our
consideration. When we add up all the accumulated relationships
between all the
successive experiences in our lives, they will always
combine cumulatively to comprise a
tetrahedron, simple or compound.
The number of telephone lines necessary to interequip
various numbers of
individuals so that any two individuals will always
have their unique private telephone line
is always (N 2 - N)/2, where N
is the number of telephones.
This is to say that all the
special interrelationships of all experiences define
comprehension, which is the number of
connections necessary to an understanding of "what everything
is all about." When we
understand, we have all the fundamental connections
between the star events of our
consideration. When we add up all the accumulated relationships
between all the
successive experiences in our lives, they will always
combine cumulatively to comprise a
tetrahedron, simple or compound.
|

|
228.00
 Scenario Principle
Scenario Principle
|

|
228.01
 Definition: The scenario principle discloses that
the Universe of total man
experience may not be simultaneously recollected and
reconsidered, but may be
progressively subdivided into a plurality of locally
tunable event foci or "points," of which
a minimum of four positive and four negative are required
as a “considerable set,” that is,
as the first finite subdivision of finite Universe.
Definition: The scenario principle discloses that
the Universe of total man
experience may not be simultaneously recollected and
reconsidered, but may be
progressively subdivided into a plurality of locally
tunable event foci or "points," of which
a minimum of four positive and four negative are required
as a “considerable set,” that is,
as the first finite subdivision of finite Universe.
|

|
228.10
 Considerable Set: All experience is reduced to nonsimultaneously
“considerable sets”; irrelevant to consideration are
all those experiences that are either too
large and therefore too infrequent, or too minuscule
and therefore too frequent, to be
tunably considerable as pertaining to the residual constellation
of approximately congruent
recollections of experiences.
Considerable Set: All experience is reduced to nonsimultaneously
“considerable sets”; irrelevant to consideration are
all those experiences that are either too
large and therefore too infrequent, or too minuscule
and therefore too frequent, to be
tunably considerable as pertaining to the residual constellation
of approximately congruent
recollections of experiences.
|

|
228.11
 A "considerable set" inherently subdivides all the
rest of irrelevant
experiences of Universe into macrocosmic and microcosmic
sets immediately outside or
immediately inside the considered set of experience
foci.
A "considerable set" inherently subdivides all the
rest of irrelevant
experiences of Universe into macrocosmic and microcosmic
sets immediately outside or
immediately inside the considered set of experience
foci.
|

|
228.12
 Scenario Principle: Considerable Set: In considering
all experiences, the
mistakes of the past and the anticipations of the future
are metaphysically irrelevant. We
do not have to be preoccupied with hypothetical or potential
experiences because we are
always living in the now. Living in the present tense
obviates impatience. (See Sec.
529.11.)
Scenario Principle: Considerable Set: In considering
all experiences, the
mistakes of the past and the anticipations of the future
are metaphysically irrelevant. We
do not have to be preoccupied with hypothetical or potential
experiences because we are
always living in the now. Living in the present tense
obviates impatience. (See Sec.
529.11.)
|

|
229.00
 Principle of Synergetic Advantage
Principle of Synergetic Advantage
|

|
229.01
 Definition: The principle of synergetic advantage
states that macro
Definition: The principle of synergetic advantage
states that macro micro
does not equal micro micro
does not equal micro macro. Synergetic advantage is
only to be effected by
macro macro. Synergetic advantage is
only to be effected by
macro micro procedure. Synergetic advantage procedures
are irreversible.
Micro micro procedure. Synergetic advantage procedures
are irreversible.
Micro macro procedures are inherently frustrated. macro procedures are inherently frustrated.
|

|
229.02
 The notion that commencing the exploration of the
unknown with unity as
one (such as Darwin's single cell) will provide simple
and reliable arithmetical
compounding (such as Darwin's theory of evolution: going
from simple
The notion that commencing the exploration of the
unknown with unity as
one (such as Darwin's single cell) will provide simple
and reliable arithmetical
compounding (such as Darwin's theory of evolution: going
from simple complex;
amoeba complex;
amoeba monkey monkey man)
is an illusion that as yet pervades
and debilitates elementary
education. man)
is an illusion that as yet pervades
and debilitates elementary
education.
|

|
229.03
 Synergy discloses that the information to be derived
from micro
Synergy discloses that the information to be derived
from micro macro
educational strategy fails completely to predict the
experimentally demonstrable
gravitational or mass-attraction integrities of entropically
irreversible, universal scenario
reality. macro
educational strategy fails completely to predict the
experimentally demonstrable
gravitational or mass-attraction integrities of entropically
irreversible, universal scenario
reality.
|

|
229.04
 Human experience discloses the eminent feasibility
of inbreeding biological
species by mating like types, such as two fast-running
horses. This concentrates the fast-
running genes in the offspring while diminishing the
number of general adaptability genes
within the integral organism. This requires the complementary
external care of the inbred
specialist through invention or employment of extracorporeal
environmental
facilities__biological or nonbiological. It is easy to
breed out metaphysical intellection
characteristics, leaving a residual concentration of
purely physical proclivities and
evoluting by further inbreeding from human to monkey.
(Witness the millions of dollars
society pays for a "prizefight" in which two organisms
are each trying to destroy the
other's thinking mechanism. This and other trends disclose
that a large segment of
humanity is evoluting toward producing the next millennia's
special breed of monkeys.)
There is no experimental evidence of the ability to
breed in the weightless, metaphysically
oriented mind and its access to conceptionings of eternal
generalized principles.
Human experience discloses the eminent feasibility
of inbreeding biological
species by mating like types, such as two fast-running
horses. This concentrates the fast-
running genes in the offspring while diminishing the
number of general adaptability genes
within the integral organism. This requires the complementary
external care of the inbred
specialist through invention or employment of extracorporeal
environmental
facilities__biological or nonbiological. It is easy to
breed out metaphysical intellection
characteristics, leaving a residual concentration of
purely physical proclivities and
evoluting by further inbreeding from human to monkey.
(Witness the millions of dollars
society pays for a "prizefight" in which two organisms
are each trying to destroy the
other's thinking mechanism. This and other trends disclose
that a large segment of
humanity is evoluting toward producing the next millennia's
special breed of monkeys.)
There is no experimental evidence of the ability to
breed in the weightless, metaphysically
oriented mind and its access to conceptionings of eternal
generalized principles.
|

|
229.05
 All known living species could be inbreedingly isolated
from humans by
environmental complementation of certain genetic proclivities
and lethal exclusion of
others, but there is no experimental evidence of any
ability to compound purely physical
proclivity genes to inaugurate metaphysical behaviors
humanity's complex metaphysical-
physical congruence with the inventory of complex behavioral
characteristics of Universe.
All known living species could be inbreedingly isolated
from humans by
environmental complementation of certain genetic proclivities
and lethal exclusion of
others, but there is no experimental evidence of any
ability to compound purely physical
proclivity genes to inaugurate metaphysical behaviors
humanity's complex metaphysical-
physical congruence with the inventory of complex behavioral
characteristics of Universe.
|

|
229.06
 Universe is the aggregate of eternal generalized principles
whose
nonunitarily conceptual scenario is unfoldingly manifest
in a variety of special cases in
local time-space transformative evolutionary events.
Humans are each a special-case
unfoldment integrity of the complex aggregate of abstract
weightless omni-
interaccommodative maximally synergetic non-sensorial
Universe of eternal timeless
principles. Humanity being a macro
Universe is the aggregate of eternal generalized principles
whose
nonunitarily conceptual scenario is unfoldingly manifest
in a variety of special cases in
local time-space transformative evolutionary events.
Humans are each a special-case
unfoldment integrity of the complex aggregate of abstract
weightless omni-
interaccommodative maximally synergetic non-sensorial
Universe of eternal timeless
principles. Humanity being a macro micro
Universe, unfolding
eventuation is physically
irreversible yet eternally integrated with Universe.
Humanity cannot shrink and return into
the womb and revert to as yet unfertilized ova. micro
Universe, unfolding
eventuation is physically
irreversible yet eternally integrated with Universe.
Humanity cannot shrink and return into
the womb and revert to as yet unfertilized ova.
|

|
229.10
 Corollary: Principle of Irreversibility: The principle
of irreversibility
states that the evolutionary process is irreversible
locally in physical "time-space"__that is,
in frequency and angle definitioning, because the antientropic
metaphysical world is not a
mirror-imaged reversal of the entropic physical world's
disorderly expansiveness.
Corollary: Principle of Irreversibility: The principle
of irreversibility
states that the evolutionary process is irreversible
locally in physical "time-space"__that is,
in frequency and angle definitioning, because the antientropic
metaphysical world is not a
mirror-imaged reversal of the entropic physical world's
disorderly expansiveness.
|

|
230.00
 Tetrahedral Number
Tetrahedral Number
|

|
230.01
 Definition: The number of balls in the longest row
of any triangular unit-
radius ball cluster will always be the same as the number
of rows of balls in the triangle,
each row always having one more than the preceding row,
and the number of balls in the
complete triangular cluster will always be
Definition: The number of balls in the longest row
of any triangular unit-
radius ball cluster will always be the same as the number
of rows of balls in the triangle,
each row always having one more than the preceding row,
and the number of balls in the
complete triangular cluster will always be
|

|
230.02
 We can stack successively rowed triangular groups
of balls on top of one
another with one ball on the top, three below that,
and six below that, as cannon balls or
oranges are stacked. Such stacks are always inherently
tetrahedral. We can say that the
sum of all the interrelationships of all our successive
experiences from birth to now__for
each individual, as well as for the history of all humanity__is
always a tetrahedral number.
We can stack successively rowed triangular groups
of balls on top of one
another with one ball on the top, three below that,
and six below that, as cannon balls or
oranges are stacked. Such stacks are always inherently
tetrahedral. We can say that the
sum of all the interrelationships of all our successive
experiences from birth to now__for
each individual, as well as for the history of all humanity__is
always a tetrahedral number.
|

|
231.00
 Principle of Universal Integrity
Principle of Universal Integrity
|

|
231.01
 Definition: The principle of universal integrity states
that the wide-arc
tensive or implosive forces of Universe always inherently
encompass the short-arc
vectorial, explosive, disintegrative forces of Universe.
Definition: The principle of universal integrity states
that the wide-arc
tensive or implosive forces of Universe always inherently
encompass the short-arc
vectorial, explosive, disintegrative forces of Universe.
|

|
231.02
 The gravitational constant will always be greater
than the radiational
constant__minutely, but always so. (For further exposition
of this principle, see Secs.
251.05,
529.03,
541 and
1052.)
The gravitational constant will always be greater
than the radiational
constant__minutely, but always so. (For further exposition
of this principle, see Secs.
251.05,
529.03,
541 and
1052.)
|

|
232.00
 Principle of Conservation of Symmetry
Principle of Conservation of Symmetry
|

|
232.01
 Definition: Whereas the tetrahedron has four symmetrically
interarrayed
poles in which the polar opposites are four vertexes
vs. four faces; and whereas the polar
axes of all other symmetrical structural systems consist
of vertex vs. vertex, or mid-edge
vs. mid-edge, or face vs. face; it is seen that only
in the case of vertex vs. face__the four
poles of the tetrahedron__do the four vertexial “points”
have polar face vacancies or
“space” into which the wavilinear coil spring legs of
the tetrahedron will permit those four
vertexes to travel. The tetrahedron is the only omnisymmetrical
structural system that can
be turned inside out. (See Secs.
624.05,
905.18 and
905.19.)
Definition: Whereas the tetrahedron has four symmetrically
interarrayed
poles in which the polar opposites are four vertexes
vs. four faces; and whereas the polar
axes of all other symmetrical structural systems consist
of vertex vs. vertex, or mid-edge
vs. mid-edge, or face vs. face; it is seen that only
in the case of vertex vs. face__the four
poles of the tetrahedron__do the four vertexial “points”
have polar face vacancies or
“space” into which the wavilinear coil spring legs of
the tetrahedron will permit those four
vertexes to travel. The tetrahedron is the only omnisymmetrical
structural system that can
be turned inside out. (See Secs.
624.05,
905.18 and
905.19.)
|

|
232.02
 Take the rubber glove that is green outside and red
inside. Stripped off, it
becomes red. The left-handedness is annihilated: inside-outing.
You do not lose the
convex-concave; all you lose is the leftness or the
rightness. Whether it is a tree or a
glove, each limb or finger is a tetrahedron.
Take the rubber glove that is green outside and red
inside. Stripped off, it
becomes red. The left-handedness is annihilated: inside-outing.
You do not lose the
convex-concave; all you lose is the leftness or the
rightness. Whether it is a tree or a
glove, each limb or finger is a tetrahedron.
|

|
232.03
 Synergetics shows that the tetrahedron can be extrapolated
into life in all its
experience phases, thus permitting humanity's entry
into a new era of cosmic awareness.
Synergetics shows that the tetrahedron can be extrapolated
into life in all its
experience phases, thus permitting humanity's entry
into a new era of cosmic awareness.
|
| Next Section: 240.00 |