
 60-Degree Coordination
60-Degree Coordination

|
423.00  60-Degree Coordination
60-Degree Coordination
|

|
423.01
 In the octet truss system, all the vectors are of
identical length and all the
angles around any convergence are the same. The patterns
repeat themselves consistently.
At every internal convergence, there are always 12 vectors
coming together, and they are
always convergent at 60 degrees with respect to the
next adjacent ones.
In the octet truss system, all the vectors are of
identical length and all the
angles around any convergence are the same. The patterns
repeat themselves consistently.
At every internal convergence, there are always 12 vectors
coming together, and they are
always convergent at 60 degrees with respect to the
next adjacent ones.
|

|
423.02
 There are angles other than 60-degrees generated in
the system, as for
instance the square equatorial mid-section of the octahedron.
These angles of other than
60-degrees occur between nonadjacently converging vectorial
connectors of the system.
The prime structural relationship is with the 60 degree
angle.
There are angles other than 60-degrees generated in
the system, as for
instance the square equatorial mid-section of the octahedron.
These angles of other than
60-degrees occur between nonadjacently converging vectorial
connectors of the system.
The prime structural relationship is with the 60 degree
angle.
|

|
423.03
 Fundamental 60-degree coordination operates either
circumferentially or
radially. This characteristic is lacking in 90-degree
coordination, where the hypotenuse of
the 90-degree angles will not be congruent and logically
integratable with the radials.
Fundamental 60-degree coordination operates either
circumferentially or
radially. This characteristic is lacking in 90-degree
coordination, where the hypotenuse of
the 90-degree angles will not be congruent and logically
integratable with the radials.
|

|
423.04
 When we begin to integrate our arithmetical identities,
as for instance n2 or
n3 , with a 60-degree coordination system, we find important
coincidence with the
topological inventories of systems, particularly with
the isotropic vector matrix which
makes possible fourth- and fifth-power modeling.
When we begin to integrate our arithmetical identities,
as for instance n2 or
n3 , with a 60-degree coordination system, we find important
coincidence with the
topological inventories of systems, particularly with
the isotropic vector matrix which
makes possible fourth- and fifth-power modeling.
|

|
423.10
 Hexagon as Average of Angular Stabilizations: The
irrational radian and
pi are not used by nature because angular accelerations
are in finite package
impellments3 which are chordal (not arcs) and produce
hexagons because the average of
all angular stabilizations from all triangular interactions
average at 60 degrees__ergo, radii
and 60-degree chords are equal and identical; ergo,
six 60-degree chords equal one
frequency cycle; ergo, one quantum. Closest packed circles
or spheres do not occupy all
area or space, but six-triangled, nucleated hexagons
do constitute the shortest route cyclic
enclosure of closest-packed nucleation and do uniformly
occupy all planar area or
volumetric space.
Hexagon as Average of Angular Stabilizations: The
irrational radian and
pi are not used by nature because angular accelerations
are in finite package
impellments3 which are chordal (not arcs) and produce
hexagons because the average of
all angular stabilizations from all triangular interactions
average at 60 degrees__ergo, radii
and 60-degree chords are equal and identical; ergo,
six 60-degree chords equal one
frequency cycle; ergo, one quantum. Closest packed circles
or spheres do not occupy all
area or space, but six-triangled, nucleated hexagons
do constitute the shortest route cyclic
enclosure of closest-packed nucleation and do uniformly
occupy all planar area or
volumetric space.
|

|
(Footnote 3: For a related concept see Secs. 1009.50, Acceleration, and 1009.60, Hammerthrower.) |

|
424.00
 Transformation by Complementary Symmetry
Transformation by Complementary Symmetry
|

|
424.01
 The octet truss complex is a precessionally nonredundant,
isotropic vector-
tensor evolutionary relationship whose energy transformation
accountings are
comprehensively rational__radially and circumferentially__to
all chemical, biological,
electromagnetic, thermodynamic, gravitational, and radiational
behaviors of nature. It
accommodates all transformations by systematic complementary
symmetries of concentric,
contractile, involutional, turbo-geared, rational, turbulence-accommodating,
inside-outing,
positive-tonegative-to-equilibrium, pulsative coordinate
displacements.
The octet truss complex is a precessionally nonredundant,
isotropic vector-
tensor evolutionary relationship whose energy transformation
accountings are
comprehensively rational__radially and circumferentially__to
all chemical, biological,
electromagnetic, thermodynamic, gravitational, and radiational
behaviors of nature. It
accommodates all transformations by systematic complementary
symmetries of concentric,
contractile, involutional, turbo-geared, rational, turbulence-accommodating,
inside-outing,
positive-tonegative-to-equilibrium, pulsative coordinate
displacements.
|

|
424.02
 Thus we see both the rational energy quantum of physics
and the topological
tetrahedron of the isotropic vector matrix rationally
accouming all physical and
metaphysical systems and their transforrnative transactins.
(See Sec. 620.12.)
Thus we see both the rational energy quantum of physics
and the topological
tetrahedron of the isotropic vector matrix rationally
accouming all physical and
metaphysical systems and their transforrnative transactins.
(See Sec. 620.12.)
|

|
424.03
 This indefinitely extending vector system in dynamic
equilibrium provides a
rational frame of reference in universal dimension for
measurement of any energy
conversion or any degree of developed energy factor
disequilibrium or its predictable
reaction developments__of impoundment or release__ ergo,
for atomic characteristics.
This indefinitely extending vector system in dynamic
equilibrium provides a
rational frame of reference in universal dimension for
measurement of any energy
conversion or any degree of developed energy factor
disequilibrium or its predictable
reaction developments__of impoundment or release__ ergo,
for atomic characteristics.
|

|
425.00
 Potentiality of Vector Equilibrium
Potentiality of Vector Equilibrium
|

|
425.01
 Where all the frequency modulations of the local vectors
are approximately
equal, we have a potentially local vector equilibrium,
but the operative vector frequency
complexity has the inherent qualities of accommodating
both proximity and remoteness in
respect to any locally initiated actions, ergo, a complex
of relative frequencies and
velocities of realization lags are accommodated (Corollary
at Sec. 240.37).
Where all the frequency modulations of the local vectors
are approximately
equal, we have a potentially local vector equilibrium,
but the operative vector frequency
complexity has the inherent qualities of accommodating
both proximity and remoteness in
respect to any locally initiated actions, ergo, a complex
of relative frequencies and
velocities of realization lags are accommodated (Corollary
at Sec. 240.37).
|

|
426.00
 Spherics
Spherics
|

|
426.01
 An isotropic vector matrix can be only omnisymmetrically,
radiantly, and
"broadcastingly" generated, that is, propagated and
radiantly regenerated, from only one
vector equilibrium origin, although it may be tuned
in, or frequency received, at any point
in Universe and thus regenerate local congruence with
any of its radiantly broadcast vector
structurings.
An isotropic vector matrix can be only omnisymmetrically,
radiantly, and
"broadcastingly" generated, that is, propagated and
radiantly regenerated, from only one
vector equilibrium origin, although it may be tuned
in, or frequency received, at any point
in Universe and thus regenerate local congruence with
any of its radiantly broadcast vector
structurings.
|

|
426.02
 An isotropic vector matrix can be only radiantly generated
at a "selectable"
(tunable) propagation frequency and vector-size (length)
modular spacing and broadcast
omnidirectionally or focally beamed outward from any
vector-center-fixed origin such that
one of its symmetrically regenerated vector-convergent
fixes will be congruent with any
other identical wavelength and frequency attuned and
radiantly reachable vector-center
fixes in Universe.
An isotropic vector matrix can be only radiantly generated
at a "selectable"
(tunable) propagation frequency and vector-size (length)
modular spacing and broadcast
omnidirectionally or focally beamed outward from any
vector-center-fixed origin such that
one of its symmetrically regenerated vector-convergent
fixes will be congruent with any
other identical wavelength and frequency attuned and
radiantly reachable vector-center
fixes in Universe.
|

|
426.03
 In time-vectorable Universe, the maximal range of
radiant-regenerative
reachability in time is determined by the omnidirectional
velocity of all radiation: c2, i.e.,
(186,000)2.4
In time-vectorable Universe, the maximal range of
radiant-regenerative
reachability in time is determined by the omnidirectional
velocity of all radiation: c2, i.e.,
(186,000)2.4
|

|
(Footnote 4: Within a week after this paragraph was drafted The New York Times of 22 November 1972 reported that the National Bureau of Standards laboratories at Boulder, Colorado, had determined the speed of light as "186,282.3960 miles per second with an estimated error margin no greater than 3.6 feet a second... Multiplying wavelength by frequency gives the speed of light.") |
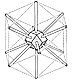 Fig. 426.04 |
426.04
 Spherics: Employing the rhombic dodecahedron as the
hub at the vector
crossings of the octet truss (the isotropic vector matrix)
provides unique economic,
technical, and geometric advantages: its 12 facets represent
the six pairs of planes
perpendicular to the six degrees of freedom. (See Sec.
537.10.)
Its 12 diamond faces also
provide the even-numbered means of allowing the vectors
to skew-weave around the
nucleus at critical-proximity distances without touching
the nucleus or one another.
Because two or more lines cannot go through the same
point at the same time, this
function of the rhombic dodecahedron's hub makes all
the difference between regenerative
success or failure of Universe.
(See Figs. 955.52 and
426.04.)
Spherics: Employing the rhombic dodecahedron as the
hub at the vector
crossings of the octet truss (the isotropic vector matrix)
provides unique economic,
technical, and geometric advantages: its 12 facets represent
the six pairs of planes
perpendicular to the six degrees of freedom. (See Sec.
537.10.)
Its 12 diamond faces also
provide the even-numbered means of allowing the vectors
to skew-weave around the
nucleus at critical-proximity distances without touching
the nucleus or one another.
Because two or more lines cannot go through the same
point at the same time, this
function of the rhombic dodecahedron's hub makes all
the difference between regenerative
success or failure of Universe.
(See Figs. 955.52 and
426.04.)
|

|
426.10
 Definition of a Spheric: A "spheric" is any one of
the rhombic dodecahedra
symmetrically recurrent throughout an isotropic-vector-matrix
geometry wherein the
centers of area of each of the rhombic dodecahedra's
12 diamond facets are exactly and
symmetrically tangent at 12 omnisymmetrically interarrayed
points Iying on the surface of
any one complete sphere, entirely contained within the
spheric-identifying rhombic
dodecahedra, with each of any such rhombic dodecahedra's
tangentially contained spheres
symmetrically radiant around every other, i.e., every
omnidirectionally alternate vertex of
every isotropic vector matrix, with the 12 points of
spherical tangency of each of the
rhombic dodecahedra exactly congruent also with the
12 vertexes of the vector
equilibrium most immediately surrounding the vertex
center of the sphere, each of whose
12 vector equilibrium radii are the special set of isotropic
vector matrix vectors leading
outwardly from the sphere's center vertex to the 12
most immediately surrounding
vertexes.
Definition of a Spheric: A "spheric" is any one of
the rhombic dodecahedra
symmetrically recurrent throughout an isotropic-vector-matrix
geometry wherein the
centers of area of each of the rhombic dodecahedra's
12 diamond facets are exactly and
symmetrically tangent at 12 omnisymmetrically interarrayed
points Iying on the surface of
any one complete sphere, entirely contained within the
spheric-identifying rhombic
dodecahedra, with each of any such rhombic dodecahedra's
tangentially contained spheres
symmetrically radiant around every other, i.e., every
omnidirectionally alternate vertex of
every isotropic vector matrix, with the 12 points of
spherical tangency of each of the
rhombic dodecahedra exactly congruent also with the
12 vertexes of the vector
equilibrium most immediately surrounding the vertex
center of the sphere, each of whose
12 vector equilibrium radii are the special set of isotropic
vector matrix vectors leading
outwardly from the sphere's center vertex to the 12
most immediately surrounding
vertexes.
|

|
426.11
 These 12 vertexes, which are omni-equidistant from
every other vertex of
the isotropic vector matrix, also occur at the diamond-face
centers of the "spheric"
rhombic dodecahedra and are also the points of tangency
of 12 uniradius spheres
immediately and omni-intertangentially surrounding (i.e.,
closest-packing) the sphere first
defined by the first rhombic dodecahedron. Each rhombic
dodecahedron symmetrically
surrounds every radiantly alternate vertex of the isotropic
vector matrix with the other
radiantly symmetrical unsurrounded set of vertexes always
and only occurring at the
diamond-face centers of the rhombic dodecahedra.
These 12 vertexes, which are omni-equidistant from
every other vertex of
the isotropic vector matrix, also occur at the diamond-face
centers of the "spheric"
rhombic dodecahedra and are also the points of tangency
of 12 uniradius spheres
immediately and omni-intertangentially surrounding (i.e.,
closest-packing) the sphere first
defined by the first rhombic dodecahedron. Each rhombic
dodecahedron symmetrically
surrounds every radiantly alternate vertex of the isotropic
vector matrix with the other
radiantly symmetrical unsurrounded set of vertexes always
and only occurring at the
diamond-face centers of the rhombic dodecahedra.
|

|
426.12
 One radiantly alternate set of vertexes of the isotropic
vector matrix always
occurs at the spheric centers of omni-closest-packed,
uniradius spheres; whereas the other
radiantly alternate set of vertexes of the isotropic
vector matrix always occurs at the
spheric intertangency points of omniclosest-packed,
uniradius spheres.
One radiantly alternate set of vertexes of the isotropic
vector matrix always
occurs at the spheric centers of omni-closest-packed,
uniradius spheres; whereas the other
radiantly alternate set of vertexes of the isotropic
vector matrix always occurs at the
spheric intertangency points of omniclosest-packed,
uniradius spheres.
|

|
426.20
 Allspace Filling: The rhombic dodecahedra symmetrically
fill allspace in
symmetric consort with the isotropic vector matrix.
Each rhombic dodecahedron defines
exactly the unique and omnisimilar domain of every radiantly
alternate vertex of the
isotropic vector matrix as well as the unique and omnisimilar
domains of each and every
interior-exterior vertex of any aggregate of closest-packed,
uniradius spheres whose
respective centers will always be congruent with every
radiantly alternate vertex of the
isotropic vector matrix, with the corresponding set
of alternate vertexes always occurAng
at all the intertangency points of the closest-packed
spheres.
Allspace Filling: The rhombic dodecahedra symmetrically
fill allspace in
symmetric consort with the isotropic vector matrix.
Each rhombic dodecahedron defines
exactly the unique and omnisimilar domain of every radiantly
alternate vertex of the
isotropic vector matrix as well as the unique and omnisimilar
domains of each and every
interior-exterior vertex of any aggregate of closest-packed,
uniradius spheres whose
respective centers will always be congruent with every
radiantly alternate vertex of the
isotropic vector matrix, with the corresponding set
of alternate vertexes always occurAng
at all the intertangency points of the closest-packed
spheres.
|

|
426.21
 The rhombic dodecahedron contains the most volume
with the least surface
of all the allspace-filling geometrical forms, ergo,
rhombic dodecahedra are the most
economical allspace subdividers of Universe. The rhombic
dodecahedra fill and
symmetrically subdivide allspace most economically,
while simultaneously, symmetrically,
and exactly defining the respective domains of each
sphere as well as the spaces between
the spheres, the respective shares of the
inter-closest-packed-sphere-interstitial
space. The
rhombic dodecahedra are called "spherics," for their
respective volumes are always the
unique closest-packed, uniradius spheres' volumetric
domains of reference within the
electively generatable and selectively "sizable" or
tunable of all isotropic vector matrixes
of all metaphysical "considering" as regeneratively
reoriginated by any thinker anywhere at
any time; as well as of all the electively generatable
and selectively tunable (sizable)
isotropic vector matrixes of physical electromagnetics,
which are also reoriginatable
physically by anyone anywhere in Universe.
The rhombic dodecahedron contains the most volume
with the least surface
of all the allspace-filling geometrical forms, ergo,
rhombic dodecahedra are the most
economical allspace subdividers of Universe. The rhombic
dodecahedra fill and
symmetrically subdivide allspace most economically,
while simultaneously, symmetrically,
and exactly defining the respective domains of each
sphere as well as the spaces between
the spheres, the respective shares of the
inter-closest-packed-sphere-interstitial
space. The
rhombic dodecahedra are called "spherics," for their
respective volumes are always the
unique closest-packed, uniradius spheres' volumetric
domains of reference within the
electively generatable and selectively "sizable" or
tunable of all isotropic vector matrixes
of all metaphysical "considering" as regeneratively
reoriginated by any thinker anywhere at
any time; as well as of all the electively generatable
and selectively tunable (sizable)
isotropic vector matrixes of physical electromagnetics,
which are also reoriginatable
physically by anyone anywhere in Universe.
|

|
426.22
 The rhombic dodecahedron's 12 diamond faces are the
12 unique planes
always occurring perpendicularly to the midpoints of
all vector radii of all the closest-
packed spheres whenever and wherever they may be metaphysically
or physically
regenerated, i.e., perpendicular to the midpoints of
all vectors of all isotropic vector
matrixing.
The rhombic dodecahedron's 12 diamond faces are the
12 unique planes
always occurring perpendicularly to the midpoints of
all vector radii of all the closest-
packed spheres whenever and wherever they may be metaphysically
or physically
regenerated, i.e., perpendicular to the midpoints of
all vectors of all isotropic vector
matrixing.
|

|
426.30
 Spherics and Modularity: None of the rhombic dodecahedra's
edges are
congruent with the vectors of the isotropic vector matrix,
and only six of the rhombic
dodecahedra's 14 vertexes are congruent with the symmetrically
co-reoccurring vertexes
of the isotropic vector matrix. The other eight vertexes
of the rhombic dodecahedra are
congruent with the centers of volume of the eight edge-interconnected
tetrahedra
omnisymmetrically and radiantly arrayed around every
vertex of the isotropic vector
matrix, with all the edges of all the tetrahedra always
congruent with all the vectors of the
isotropic vector matrix, and all the vertexes of all
the tetrahedra always congruent with the
vertexes of the isotropic vector matrix, all of which
vertexes are always most economically
interconnected by three edges of the tetrahedra.
Spherics and Modularity: None of the rhombic dodecahedra's
edges are
congruent with the vectors of the isotropic vector matrix,
and only six of the rhombic
dodecahedra's 14 vertexes are congruent with the symmetrically
co-reoccurring vertexes
of the isotropic vector matrix. The other eight vertexes
of the rhombic dodecahedra are
congruent with the centers of volume of the eight edge-interconnected
tetrahedra
omnisymmetrically and radiantly arrayed around every
vertex of the isotropic vector
matrix, with all the edges of all the tetrahedra always
congruent with all the vectors of the
isotropic vector matrix, and all the vertexes of all
the tetrahedra always congruent with the
vertexes of the isotropic vector matrix, all of which
vertexes are always most economically
interconnected by three edges of the tetrahedra.
|

|
426.31
 A spheric is any one of the rhombic dodecahedra, the
center of each of
whose 12 diamond facets is exactly tangent to the surface
of each sphere formed
equidistantly around each vertex of the isotropic vector
matrix.
A spheric is any one of the rhombic dodecahedra, the
center of each of
whose 12 diamond facets is exactly tangent to the surface
of each sphere formed
equidistantly around each vertex of the isotropic vector
matrix.
|

|
426.32
 A spheric has 144 A and B modules, and there are 24
A Quanta Modules
(see
Sec. 920
and 940)
in the tetrahedron, which equals
l/6th of a spheric. Each of the
tetrahedron's 24 modules contains 1/144th of a sphere,
plus 1/l44th of the nonsphere
space unique to the individual domain of the specific
sphere of which it is a l/144th part,
and whose spheric center is congruent with the most
acute-angle vertex of each and all of
the A and B Quanta Modules. The four corners of the
tetrahedron are centers of four
embryonic (potential) spheres.
A spheric has 144 A and B modules, and there are 24
A Quanta Modules
(see
Sec. 920
and 940)
in the tetrahedron, which equals
l/6th of a spheric. Each of the
tetrahedron's 24 modules contains 1/144th of a sphere,
plus 1/l44th of the nonsphere
space unique to the individual domain of the specific
sphere of which it is a l/144th part,
and whose spheric center is congruent with the most
acute-angle vertex of each and all of
the A and B Quanta Modules. The four corners of the
tetrahedron are centers of four
embryonic (potential) spheres.
|

|
426.40
 Radiant Valvability of Isotropic-Vector-Matrix-Defined
Wavelength:
We can resonate the vector equilibrium in many ways.
An isotropic vector matrix may be
both radiantly generated and regenerated from any vector-centered
fixed origin in
Universe such that one of its vertexes will be congruent
with any other radiantly reachable
center fix in Universe; i.e., it can communicate with
any other noninterfered-with point in
Universe. The combined reachability range is determined
by the omnidirectional velocity
of all radiation, c2 within the availably investable
time.
Radiant Valvability of Isotropic-Vector-Matrix-Defined
Wavelength:
We can resonate the vector equilibrium in many ways.
An isotropic vector matrix may be
both radiantly generated and regenerated from any vector-centered
fixed origin in
Universe such that one of its vertexes will be congruent
with any other radiantly reachable
center fix in Universe; i.e., it can communicate with
any other noninterfered-with point in
Universe. The combined reachability range is determined
by the omnidirectional velocity
of all radiation, c2 within the availably investable
time.
|

|
426.41
 The rhombic dodecahedron's 144 modules may be reoriented
within it to be
either radiantly disposed from the contained sphere's
center of volume or circumferentially
arrayed to serve as the interconnective pattern of six
1/6th-spheres, with six of the
dodecahedron's 14 vertexes congruent with the centers
of the six individual l/6th spheres
that it interconnects. The six l/6th spheres are completed
when 12 additional rhombic
dodecahedra are close-packed around it.
The rhombic dodecahedron's 144 modules may be reoriented
within it to be
either radiantly disposed from the contained sphere's
center of volume or circumferentially
arrayed to serve as the interconnective pattern of six
1/6th-spheres, with six of the
dodecahedron's 14 vertexes congruent with the centers
of the six individual l/6th spheres
that it interconnects. The six l/6th spheres are completed
when 12 additional rhombic
dodecahedra are close-packed around it.
|

|
426.42
 The fact that the rhombic dodecahedron can have its
144 modules oriented
as either introvert-extrovert or as three-way circumferential
provides its valvability
between broadcasting-transceiving and noninterference
relaying. The first radio tuning
crystal must have been a rhombic dodecahedron.
The fact that the rhombic dodecahedron can have its
144 modules oriented
as either introvert-extrovert or as three-way circumferential
provides its valvability
between broadcasting-transceiving and noninterference
relaying. The first radio tuning
crystal must have been a rhombic dodecahedron.
|

|
426.43
 Multiplying wavelength by frequency equals the speed
of light. We have two
experimentally demonstrable radiational variables. We
have to do whatever we do against
time. Whatever we may be, each we has only so much commonly
experienceable time in
scenario Universe within which to articulate thus and
so. Therefore, the vector
equilibrium's radiant or gravitational "realizations"
are always inherently geared to or
tuned in with the fundamental time-sizing of = 186,000
mps (approximately), which unique time-size-
length increments of available time can be divided into
any desirable frequency. One
second is a desirable, commonly experienceable increment
to use, and within each unit of
it we can reach = 186,000 miles (approximately) in any non-frequency-interferedwith
direction.
Multiplying wavelength by frequency equals the speed
of light. We have two
experimentally demonstrable radiational variables. We
have to do whatever we do against
time. Whatever we may be, each we has only so much commonly
experienceable time in
scenario Universe within which to articulate thus and
so. Therefore, the vector
equilibrium's radiant or gravitational "realizations"
are always inherently geared to or
tuned in with the fundamental time-sizing of = 186,000
mps (approximately), which unique time-size-
length increments of available time can be divided into
any desirable frequency. One
second is a desirable, commonly experienceable increment
to use, and within each unit of
it we can reach = 186,000 miles (approximately) in any non-frequency-interferedwith
direction.
|

|
426.44
 Wavelength times frequency is the speed of all radiation.
If the frequency of
the vector equilibrium is four, its vector radius, or
basic wavelength = 186,000 / 4 miles
reachable within one second = 46,500 reach-miles. Electromagnetically
speaking, the
unarticulated vector equilibrium's onesecond vector
length is always 186,282.396 miles.
Wavelength times frequency is the speed of all radiation.
If the frequency of
the vector equilibrium is four, its vector radius, or
basic wavelength = 186,000 / 4 miles
reachable within one second = 46,500 reach-miles. Electromagnetically
speaking, the
unarticulated vector equilibrium's onesecond vector
length is always 186,282.396 miles.
|

|
426.45
 We multiply our frequency by the number of times we
divide the vector of
the vector equilibrium, and that gives c2 ; our reachable
points in Universe will multiply at
a rate of F2 × 10 + 2.
We multiply our frequency by the number of times we
divide the vector of
the vector equilibrium, and that gives c2 ; our reachable
points in Universe will multiply at
a rate of F2 × 10 + 2.
|

|
426.46
 All the relative volumetric intervaluations of all
the symmetric polyhedra and
of all uniradius, closest-packed spheres are inherently
regenerated in omnirational respect
to isotropic vector matrixes, whether the matrixes are
inadvertently__i.e., subjectively__
activated by the size-selective, metaphysical-consideration
initiatives, whether they are
objectively and physically articulated in consciously
tuned electromagnetic transmission, or
whether they are selectively tuned to receive on that
isotropic-vector-matrix-defined
"wavelength."
All the relative volumetric intervaluations of all
the symmetric polyhedra and
of all uniradius, closest-packed spheres are inherently
regenerated in omnirational respect
to isotropic vector matrixes, whether the matrixes are
inadvertently__i.e., subjectively__
activated by the size-selective, metaphysical-consideration
initiatives, whether they are
objectively and physically articulated in consciously
tuned electromagnetic transmission, or
whether they are selectively tuned to receive on that
isotropic-vector-matrix-defined
"wavelength."
|

|
426.47
 Humans may be quite unconscious of their unavoidable
employment of
isotropic vector matrix fields of thought or of physical
articulations; and they may
oversimplify or be only subconsciously attuned to employ
their many cosmically
intertunable faculties and especially their conceptual
and reasoning faculties. However,
their physical brains, constituted of quadrillions times
quadrillions of atoms, are always
and only most economically interassociative, interactive,
and intertransforming only in
respect to the closestpacked isotropic vector matrix
fields which altogether subconsciously
accommodate the conceptual geometry picturing and memory
storing of each individual's
evolutionary accumulation of special-case experience
happenings, which human
inventories are accumulatingly stored isotropic-vector-matrix
wise in the brain and are
conceptually retrievable by brain and are both subconsciously
and consciously
reconsidered reflexively or by reflex-shunning mind.
Humans may be quite unconscious of their unavoidable
employment of
isotropic vector matrix fields of thought or of physical
articulations; and they may
oversimplify or be only subconsciously attuned to employ
their many cosmically
intertunable faculties and especially their conceptual
and reasoning faculties. However,
their physical brains, constituted of quadrillions times
quadrillions of atoms, are always
and only most economically interassociative, interactive,
and intertransforming only in
respect to the closestpacked isotropic vector matrix
fields which altogether subconsciously
accommodate the conceptual geometry picturing and memory
storing of each individual's
evolutionary accumulation of special-case experience
happenings, which human
inventories are accumulatingly stored isotropic-vector-matrix
wise in the brain and are
conceptually retrievable by brain and are both subconsciously
and consciously
reconsidered reflexively or by reflex-shunning mind.
|
| Next Section: 427.00 |