986.410 T Quanta Module

Fig. 986.411A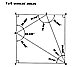

Fig. 986.411B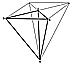

Fig. 986.411C 		986.411 The respective 12 and 30 pentahedra OABAB of the rhombic dodecahedron and the triacontahedron may be symmetrically subdivided into four right-angled tetrahedra ABCO, the point C being surrounded by three right angles ABC, BCO, and ACO. Right- angle ACB is on the surface of the rhombic-hedra system and forms the face of the tetrahedron ABCO, while right angles BCO and ACO are internal to the rhombic-hedra system and from two of the three internal sides of the tetrahedron ABCO. The rhombic dodecahedron consists of 48 identical tetrahedral modules designated ABCOd. The triacontahedron consists of 120 (60 positive and 60 negative) identical tetrahedral modules designated ABCOt, for which tetrahedron ABCOt we also introduce the name T Quanta Module.
986.412 The primitive tetrahedron of volume 1 is subdivisible into 24 A Quanta Modules. The triacontahedron of exactly tetravolume 5, has the maximum-limit case of identical tetrahedral subdivisibility__i.e., 120 subtetra. Thus we may divide the 120 subtetra population of the symmetric triacontahedron by the number 24, which is the identical subtetra population of the primitive omnisymmetrical tetrahedron: 120/24=5. Ergo, volume of the A Quanta Module = volume of the T Quanta Module.

Fig. 986.413 		986.413 The rhombic dodecahedron has a tetravolume of 6, wherefore each of its 48 identical, internal, asymmetric, component tetrahedra ABCOd has a regular tetravolume of 6/48 = 1/8 The regular tetrahedron consists of 24 quanta modules (be they A, B, C, D,5 * or T Quanta Modules; therefore ABCOd, having l/8-tetravolume, also equals three quanta modules. (See Fig. 986.413.)

(Footnote 5: C Quanta Modules and D Quanta Modules are added to the A and B Quanta Modules to compose the regular tetrahedron as shown in drawing B of Fig. 923.10.)
986.414 The vertical central-altitude line of the regular, primitive, symmetrical tetrahedron may be uniformly subdivided into four vertical sections, each of which we may speak of as quarter-prime-tetra altitude units-each of which altitude division points represent the convergence of the upper apexes of the A, B, C, D, A', B', C', D', A", B", C", D" . . . equivolume modules (as illustrated in Fig. 923.10B where__prior to the discovery of the E "Einstein" Module__additional modules were designated E through H, and will henceforth be designated as successive ABCD, A'B'C'D', A"B"C"D" . . . groups). The vertical continuance of these unit-altitude differentials produces an infinite series of equivolume modules, which we identify in vertical series continuance by groups of four repetitive ABCD groups, as noted parenthetically above. Their combined group-of- four, externally protracted, altitude increase is always equal to the total internal altitude of the prime tetrahedron.
986.415 The rhombic triacontahedron has a tetravolume of 5, wherefore each of its 120 identical, internal, asymmetric, component tetrahedra ABCOt, the T Quanta Module, has a tetravolume of 5/120 = 1/24 tetravolume__ergo, the volume of the T Quanta Module is identical to that of the A and B Quanta Modules. The rhombic dodecahedron's 48 ABCOd asymmetric tetrahedra equal three of the rhombic triacontahedron's 120 ABCOt , T Quanta Module asymmetric tetrahedra. The rhombic triacontahedron's ABCOt T Quanta Module tetrahedra are each 1/24 of the volume of the primitive "regular" tetrahedron__ergo, of identical volume to the A Quanta Module. The A Mod, like the T Mod, is structurally modeled with one of its four corners omnisurrounded by three right angles.
986.416 1 A Module = 1 B Module = 1 C Module = 1 D Module = 1 T Module = any one of the unit quanta modules of which all the hierarchy of concentric, symmetrical polyhedra of the VE family are rationally comprised. (See Sec. 910).
986.417 I find that it is important in exploratory effectiveness to remember__as we find an increasingly larger family of equivolume but angularly differently conformed quanta modules__that our initial exploration strategy was predicated upon our generalization of Avogadro's special-case (gaseous) discovery of identical numbers of molecules per unit volume for all the different chemical-element gases when individually considered or physically isolated, but only under identical conditions of pressure and heat. The fact that we have found a set of unit-volume, all-tetrahedral modules__the minimum-limit structural systems__from which may be aggregated the whole hierarchy of omnisymmetric, primitive, concentric polyhedra totally occupying the spherically spun and interspheric accommodation limits of closest-packable nuclear domains, means that we have not only incorporated all the min-max limit-case conditions, but we have found within them one unique volumetric unit common to all their primitive conformational uniqueness, and that the volumetric module was developed by vectorial__i.e., energetic__polyhedral-system definitions.
986.418 None of the tetrahedral quanta modules are by themselves allspace-filling, but they are all groupable in units of three (two A's and one B__which is called the Mite) to fill allspace progressively and to combine these units of three in nine different ways__all of which account for the structurings of all but one of the hierarchy of primitive, omniconcentric, omnisymmetrical polyhedra. There is one exception, the rhombic triacontahedron of tetravolume 5__i.e., of 120 quanta modules of the T class, which T Quanta Modules as we have learned are of equivolume to the A and B Modules.

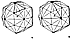Fig. 986.419 		986.419 The 120 T Quanta Modules of the rhombic triacontahedron can be grouped in two different ways to produce two different sets of 60 tetrahedra each: the 60 BAAO tetrahedra and the 60 BBAO tetrahedra. But rhombic triacontahedra are not allspace-filling polyhedra. (See Fig. 986.419.)
Next Section: 986.420
Copyright © 1997 Estate of R. Buckminster Fuller