Min-max Limit Hierarchy of Pre-time-size Allspace-fillers
|
|
986.420
Min-max Limit Hierarchy of Pre-time-size Allspace-fillers
|
 Fig. 986.421 |
986.421
Of all the allspace-filling module components, the
simplest are the three-
quanta-module Mites, consisting of two A Quanta Modules
(one A positive and one A
negative) and of one B Quanta Module (which may be either
positive or negative). Thus a
Mite can be positive or negative, depending on the sign
of its B Quanta Module. The
Mites are not only themselves tetrahedra (the minimum-sided
polyhedra), but they are also
the simplest minimum-limit case of allspace-filling
polyhedra of Universe, since they
consist of two energy-conserving A Quanta Modules and
one equivolume energy-
dispersing B Quanta Module. The energy conservation
of the A Quanta Module is
provided geometrically by its tetrahedral form: four
different right-triangled facets being
all foldable from one unique flat-out whole triangle
(Fig. 913.01),
which triangle's
boundary edges have reflective properties that bounce
around internally to those triangles
to produce similar smaller triangles: Ergo, the A Quanta
Module acts as a local energy
holder. The B Quanta Module is not foldable out of one
whole triangle, and energies
bouncing around within it tend to escape. The B Quanta
Module acts as a local energy
dispenser. (See Fig.
986.421.)
|
 MITE |
986.422
Mite: The simplest allspace-filler is the Mite (see
Secs.
953
and
986.418).
The positive Mite consists of 1 A + mod, 1 A - mod,
and B + mod; the negative Mite
consists of 1 A + mod, 1A - mod, and B-mod. Sum-total
number of modules...3.
|
|
|
986.423
Around the four corners of the tetrahedral Mites are
three right triangles.
Two of them are similar right triangles with differently
angled acute corners, and the third
right triangle around that omni-right-angled corner
is an isosceles.
|
|
|
986.424
The tetrahedral Mites may be inter-edge-bonded to fill
allspace, but only
because the spaces between them are inadvertent capturings
of Mite-shaped vacancies.
Positive Mite inter-edge assemblies produce negative
Mite vacancies, and vice versa. The
minimum-limit case always provides inadvertent entry
into the Negative Universe. Sum-
total number of
modules is...1½
|
|
|
986.425
Mites can also fill allspace by inter-face-bonding
one positive and one
negative Mite to produce the Syte. This trivalent inter-face-bonding
requires twice as
many Mites as are needed for bivalent inter-edge-bonding.
Total number of
modules is...3
|
|
|
986.426
Syte: The next simplest allspace-filler is the Syte.
(See Sec.
953.40.) Each
Syte consists of one of only three alternate ways of
face-bonding two Mites to form an
allspace-filling polyhedron, consisting of 2 A + mods,
2 A - mods, 1 B + mod, and 1 B -
mod. Sum-total number of
modules...6
|
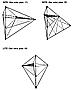 Fig. 986.427 |
986.427
Two of the three alternate ways of combining two Mites
produce tetrahedral
Sytes of one kind:
BITE (See color plate 17), RITE (See color plate 19) while the third alternate method of combining will produce a hexahedral Syte. LITE (See color plate 18) |
|
|
986.428
Kite: The next simplest allspace-filler is the Kite.
Kites are pentahedra or
half-octahedra or half-Couplers, each consisting of
one of the only two alternate ways of
combining two Sytes to produce two differently shaped
pentahedra, the Kate and the Kat,
each of 4 A + mods, 4 A - mods, 2 B + mods, and 2 B-mods.
Sum-total number of
modules...12
|
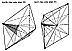 Fig. 986.429 |
986.429
Two Sytes combine to produce two Kites as
KATE (See color plate 20) KAT (See color plate 21)
|
| Next Section: 986.430 |