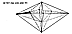
Fig. 986.340 		986.430 Octet: The next simplest allspace-filler is the Octet, a hexahedron consisting of three Sytes__ergo, 6 A + mods, 6 A - mods, 3 B + mods, and 3 B-mods. Sum-total number of modules...18

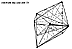Fig. 986.431 		986.431 Coupler: The next simplest allspace-filler is the Coupler, the asymmetric octahedron. (See Secs. 954.20-.70.) The Coupler consists of two Kites__ergo, 8 A + mods, 8 A - mods, 4 B + mods, and 4 B - mods. Sum-total number of modules...24

Fig. 986.432 		986.432 Cube: The next simplest allspace-filler is the Cube, consisting of four Octets__ergo, 24 A + mods, 24 A - mods, 12 B + mods, and 12 B - mods. Sum-total number of modules...72

Fig. 986.433 		986.433 Rhombic Dodecahedron: The next and last of the hierarchy of primitive allspace-fillers is the rhombic dodecahedron. The rhombic dodecahedron is the domain of a sphere (see Sec. 981.13). The rhombic dodecahedron consists of 12 Kites__ergo, 48 A + mods, 48 A - mods, 24 B + mods, and 24 B - mods. Sum-total number of modules...144
986.434 This is the limit set of simplest allspace-fillers associable within one nuclear domain of closest-packed spheres and their respective interstitial spaces. There are other allspace-fillers that occur in time-size multiplications of nuclear domains, as for instance the tetrakaidecahedron. (Compare Sec. 950.12.)
986.440 Table: Set of Simple Allspace-fillers This completes one spheric domain (i.e., sphere plus interstitial space) of one unit-radius sphere in closest packing, each sphere being centered at every other vertex of the isotropic vector matrix.
Name:Face
Triangles		Type
Hedra		A
Quanta
Modules		B
Quanta
Modules		Sum-
Total
Modules
MITE 4 tetrahedron 2 1 3
SYTE
BITE 4 tetrahedron 4 2 6
RITE 4 tetrahedron 4 2 6
LITE 6 hexahedron 4 2 6
KITE
KATE 5 pentahedron 8 4 12
KAT 5 pentahedron 8 4 12
OCTET 6 hexahedron 12 6 18
COUPLER 8 octahedron 16 8 24
CUBE 6 hexahedron 48 24 72
RHOMBIC
DODECAHEDRON		 12 dodecahedron 96 48 144


(For the minimum time-size special case realizations of the two-frequency systems. multiply each of the above Quanta Module numbers by eight.)
986.450 Energy Aspects of Spherical Modular Arrays
986.451 The rhombic dodecahedron has an allspace-filling function as the domain of any one sphere in an aggregate of unit-radius, closest-packed spheres; its 12 mid-diamond- face points C are the points of intertangency of all unit-radius, closest-packed sphere aggregates; wherefore that point C is the midpoint of every vector of the isotropic vector matrix, whose every vertex is the center of one of the unit-radius, closest-packed spheres.
986.452 These 12 inter-closest-packed-sphere-tangency points__the C points__are the 12 exclusive contacts of the "Grand Central Station" through which must pass all the great-circle railway tracks of most economically interdistanced travel of energy around any one nuclear center, and therefrom__through the C points__to other spheres in Universe. These C points of the rhombic dodecahedron's mid-diamond faces are also the energetic centers-of-volume of the Couplers, within which there are 56 possible unique interarrangements of the A and B Quanta Modules.
986.453 We next discover that two ABABO pentahedra of any two tangentially adjacent, closest-packed rhombic dodecahedra will produce an asymmetric octahedron OABABO' with O and O' being the volumetric centers (nuclear centers) of any two tangentially adjacent, closest-packed, unit-radius spheres. We call this nucleus-to-nucleus, asymmetric octahedron the Coupler, and we found that the volume of the Coupler is exactly equal to the volume of one regular tetrahedron__i.e., 24 A Quanta Modules. We also note that the Coupler always consists of eight asymmetric and identical tetrahedral Mites, the minimum simplex allspace-filling of Universe, which Mites are also identifiable with the quarks (Sec. 1052.360).
986.454 We then discover that the Mite, with its two energy-conserving A Quanta Modules and its one energy-dispersing B Quanta Module (for a total combined volume of three quanta modules), serves as the cosmic minimum allspace-filler, corresponding elegantly (in all ways) with the minimum-limit case behaviors of the nuclear physics' quarks. The quarks are the smallest discovered "particles"; they always occur in groups of three, two of which hold their energy and one of which disperses energy. This quite clearly identifies the quarks with the quanta module of which all the synergetics hierarchy of nuclear concentric symmetric polyhedra are co-occurrent.
986.455 In both the rhombic triacontahedron of tetravolume 5 and the rhombic dodecahedron of tetravolume 6 the distance from system center O at AO is always greater than CO, and BO is always greater than AO.
986.456 With this information we could reasonably hypothesize that the triacontahedron of tetravolume 5 is that static polyhedral progenitor of the only- dynamically-realizable sphere of tetravolume 5, the radius of which (see Fig. 986.314) is only 0.04 of unity greater in length than is the prime vector radius OC, which governs the dimensioning of the triacontahedron's 30 midface cases of 12 right-angled corner junctions around mid-diamond-vertex C, which provides the 12 right angles around C-the four right-angled corners of the T Quanta Module's ABC faces of their 120 radially arrayed tetrahedra, each of which T Quanta Module has a volume identical to that of the A and B Quanta Modules.
986.457 We also note that the radius OC is the same unitary prime vector with which the isotropic vector matrix is constructed, and it is also the VE unit-vector-radius distance outwardly from O, which O is always the common system center of all the members of the entire cosmic hierarchy of omniconcentric, symmetric, primitive polyhedra. In the case of the rhombic triacontahedron the 20 OA lines' distances outwardly from O are greater than OC, and the 12 OB lines' distances are even greater in length outwardly from O than OA. Wherefore I realized that, when dynamically spun, the greatcircle chord lines AB and CB are centrifugally transformed into arcs and thus sprung apart at B, which is the outermost vertex__ergo, most swiftly and forcefully outwardly impelled. This centrifugal spinning introduces the spherical excess of 6 degrees at the spherical system vertex B. (See Fig. 986.405) Such yielding increases the spheric appearance of the spun triacontahedron, as seen in contradistinction to the diamond-faceted, static, planar-bound, polyhedral state aspect.
986.458 The corners of the spherical triacontahedron's 120 spherical arc-cornered triangles are 36 degrees, 60 degrees and 90 degrees, having been sprung apart from their planar-phase, chorded corners of 31.71747441 degrees, 58.28252559 degrees, and 90 degrees, respectively. Both the triacontahedron's chorded and arced triangles are in notable proximity to the well-known 30-, 60-, and 90-degree-cornered draftsman's flat, planar triangle. I realized that it could be that the three sets of three differently-distanced- outwardly vertexes might average their outward-distance appearances at a radius of only four percent greater distance from O-thus producing a moving-picture-illusioned "dynamic" sphere of tetravolume 5, having very mildly greater radius than its static, timeless, equilibrious, rhombic triacontahedron state of tetravolume 5 with unit-vector- radius integrity terminaled at vertex C.
986.459 In the case of the spherical triacontahedron the total spherical excess of exactly 6 degrees, which is one-sixtieth of unity = 360 degrees, is all lodged in one corner. In the planar case 1.71747441 degrees have been added to 30 degrees at corner B and subtracted from 60 degrees at corner A. In both the spherical and planar triangles__as well as in the draftsman's triangle__the 90-degree corners remain unchanged.
986.460 The 120 T Quanta Modules radiantly arrayed around the center of volume of the rhombic triacontahedron manifest the most spherical appearance of all the hierarchy of symmetric polyhedra as defined by any one of the seven axially rotated, great circle system polyhedra of the seven primitive types of great-circle symmetries.
986.461 What is the significance of the spherical excess of exactly 6 degrees? In the transformation from the spherical rhombic triacontahedron to the planar triacontahedron each of the 120 triangles releases 6 degrees. 6 × 120 = 720. 720 degrees = the sum of the structural angles of one tetrahedron = 1 quantum of energy. The difference between a high-frequency polyhedron and its spherical counterpart is always 720 degrees, which is one unit of quantum__ergo, it is evidenced that spinning a polyhedron into its spherical state captures one quantum of energy__and releases it when subsiding into its pre-time- size primitive polyhedral state.
986.470 Geodesic Modular Subdivisioning

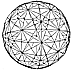Fig. 986.471 		986.471 A series of considerations leads to the definition of the most spherical- appearing limit of triangular subdivisioning:
  1. recalling that the experimentally demonstrable "most spherically-appearing" structure is always in primitive reality a polyhedron;
  2. recalling that the higher the modular frequency of a system the more spheric it appears, though it is always polyhedral and approaching not a "true sphere" limit but an unlimited multiplication of its polyhedral facetings;
  3. recalling that the 120 outer surface triangles of the icosahedron's 15 great circles constitute the cosmic maximum limit of system-surface omni-triangular- self-subdivisioning into centrally collected tetrahedron components; and
  4. recalling that the icosahedron's 10- and 6-great-circle equators of spin further subdivide the 15 great circles' outer 120 LCD triangles into four different right triangles, ADC, CDE, CFE, and EFB (see Fig. 901.03),
then it becomes evident that the icosahedron's three sets of symmetrical greatcircle spinnabilities__i.e., 6 + 10 + 15 (which totals 31 great circle self-halvings)__generate a total of 242 unit-radius, external vertexes, 480 external triangles, and 720 internal triangles (which may be considered as two congruent internal triangles, each being one of the internal triangular faces of the 480 tetrahedra whose 480 external triangular faces are showing-in which case there are 1440 internal triangles). The 480 tetrahedra consist of 120 OCAD, 120 OCDE, 120 OCEF, and 120 OFEB tetrahedra. (See Fig. 986.471.) The 480 internal face-congruent tetrahedra therefore constitute the "most spheric-appearing" of all the hemispheric equators' self-spun, surface-subdividing entirely into triangles of all the great circles of all the primitive hierarchy of symmetric polyhedra.
986.472 In case one thinks that the four symmetrical sets of the great circles of the spherical VE (which total 25 great circles in all) might omnisubdivide the system surface exclusively into a greater number of triangles, we note that some of the subdivision areas of the 25 great circles are not triangles (see quadrant BCEF in Fig. 453.01 __third printing of Synergetics 1__of which quadrangles there are a total of 48 in the system); and note that the total number of triangles in the 25-great-circle system is 288__ergo, far less than the 31 great circles' 480 spherical right triangles; ergo, we become satisfied that the icosahedron's set of 480 is indeed the cosmic maximum-limit case of system-self-spun subdivisioning of its self into tetrahedra, which 480 consist of four sets of 120 similar tetrahedra each.
986.473 It then became evident (as structurally demonstrated in reality by my mathematically close-toleranced geodesic domes) that the spherical trigonometry calculations' multifrequenced modular subdividing of only one of the icosahedron's 120 spherical right triangles would suffice to provide all the basic trigonometric data for any one and all of the unit-radius vertex locations and their uniform interspacings and interangulations for any and all frequencies of modular subdividings of the most symmetrical and most economically chorded systems' structuring of Universe, the only variable of which is the special case, time-sized radius of the special-case system being considered.
986.474 This surmise regarding nature's most-economical, least-effort design strategy has been further verified by nature's own use of the same geodesics mathematics as that which I discovered and employed in my domes. Nature has been using these mathematical principles for eternity. Humans were unaware of that fact. I discovered these design strategies only as heretofore related, as an inadvertent by-product of my deliberately undertaking to find nature's coordination system. That nature was manifesting icosahedral and VE coordinate patterning was only discovered by other scientists after I had found and demonstrated geodesic structuring, which employed the synergetics' coordinate-system strategies. This discovery by others that my discovery of geodesic mathematics was also the coordinate system being manifest by nature occurred after I had built hundreds of geodesic structures around the world and their pictures were widely published. Scientists studying X-ray diffraction patterns of protein shells of viruses in 1959 found that those shells disclosed the same patterns as those of my widely publicized geodesic domes. When Dr. Aaron Klug of the University of London__who was the one who made this discovery__communicated with me, I was able to send him the mathematical formulae for describing them. Klug explained to me that my geodesic structures are being used by nature in providing the "spherical" enclosures of her own most critical design-controlling programming devices for realizing all the unique biochemical structurings of all biology__which device is the DNA helix.
986.475 The structuring of biochemistry is epitomized in the structuring of the protein shells of all the viruses. They are indeed all icosahedral geodesic structures. They embracingly guard all the DNA-RNA codified programming of all the angle-and-frequency designing of all the biological, life-accommodating, life-articulating structures. We find nature employing synergetics geometry, and in particular the high-frequency geodesic "spheres," in many marine organisms such as the radiolaria and diatoms, and in structuring such vital organs as the male testes, the human brain, and the eyeball. All of these are among many manifests of nature's employment on her most critically strategic occasions of the most cosmically economical, structurally effective and efficient enclosures, which we find are always mathematically based on multifrequency and three-way-triangular gridding of the "spherical"__because high-frequenced__icosahedron, octahedron, or tetrahedron.
986.476 Comparing the icosahedron, octahedron, and tetrahedron-the icosahedron gives the most volume per unit weight of material investment in its structuring; the high- frequency tetrahedron gives the greatest strength per unit weight of material invested; and the octahedron affords a happy__but not as stable-mix of the two extremes, for the octahedron consists of the prime number 2, 22 = 4; whereas the tetrahedron is the odd prime number 1 and the icosahedron is the odd prime number 5. Gear trains of even number reciprocate, whereas gear trains of an odd number of gears always lock; ergo, the tetrahedral and icosahedral geodesic systems lock-fasten all their structural systems, and the octahedron's compromise, middle-position structuring tends to yield transformingly toward either the tetra or the icosa locked-limit capabilities__either of which tendencies is pulsatively propagative.
Next Section: 986.480
Copyright © 1997 Estate of R. Buckminster Fuller