Lynnclaire Dennis' Geometry:
The Pattern

Lynnclaire Dennis has many interesting ideas about geometric and nature. I am helping Lynnclaire explore these ideas. My particular interest is in finding connections between the geometry and physics.

Lynnclaire has told me that it would be interesting to explore a specific polyhedron inside another polyhedron. The inner most polyhedron had 48 cones of light coming out of it at 48 vertices. This polyhedron had 144 triangular faces. The outer polyhedron had 120 triangular faces.

48 cones of light emerge from the center polyhedron, penertate the outer polyhedron, turn around and re-enter the outer polyhedron. Then, in the space between the two polyehdra, the light/energy ties itself into a knot pattern.

These are some images of the knot pattern Lynnclaire described to me from different perspectives.

Research and Information

Note that I have not tried to record the dates for each of the items below. Therefore, they are not necessarily in any particular order.

NOTE: Some of the animations require JavaScript to be enable (one of your browser's options that could be turned off.) If you are unable to play an animation, check that your web browser has JavaScript enabled.

	This is a presentation I gave at the University of Arizona in Tucson on (09-26-2007).
	Looking at the "double" and "triple" torus and the different torus knots. Maybe the Mereon knot is "simplest" knot. (03-11-2004)
	Looking at the formation of the Pattern Knot by intersecting spirals at various angles of intersection. (09-26-2003)
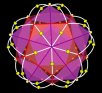
	Looking at another 120 Polyhedron made out of 5 intersecting Jitterbugs. The dynamics are very interesting. (02-16-2003)
	Here is enumerate all the possible Lynnclaire-like knots. There are 3 different knots. I also comment on the important role that twist tension in a knot plays in energy minimization configuration simulations. (07-02-2002)
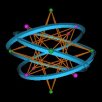
	Playing with some wire models of the Pattern Knot lead me to see how it relates to the Octahedron. (07-01-2002)
	While exploring the dual polyhedra dynamics of the Cube and the Octahedron, I discovered that the Pattern knot fits exactly the initial position of these 2 polyhedra. (06-23-2002)
	Here is a pictorial presentation of all the basic polyhedra in the 120 Polyhedron. (06-08-2002)
	From the old pattern.org web site: "Genesis of the Geometry". Some of this info is now considered at best to be incomplete. (05-21-2002)
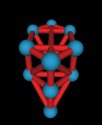
	I saw the Tree of Life in a book on crop circles and started to think that this might actually be a 3D figure. Here is an initial investigation. (03-19-2002)
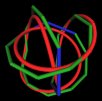
	We have been looking for the way that the Pattern Knot could be formed within the 120 Polyhedron. Here I trace out the path of the Pattern Knot using the vertices and edges of the 120 Polyhedron. (03-12-2002)
	Investigations into the creation of the Pattern Knot using helices, cones and spirals. (03-09-2002)
	The Cymatics work of Hans Jenny, creating structure out of sound waves, is very relevant to...well, everything.
	Exploring the way the Icosahedron and the Dodecahedron scale and pack together.
	The Jitterbug seems to be taking center stage as the basic motion, particularly in defining the polyhedra. Here I explore some rotational behavior. Is there a connection to Quantum Mechanics?
	Here I explore the various layers in the 120 Polyhedron. Some interesting spacing sequences are found. But is there any application to be made of this information??
	Finally, I've organized and provide here all the coordinates and vertex, edge and face maps for all the polyhedra in the120 polyhedron.
	Here is a presentation I did at the 62rd Technology Conference, Oct. 25-26, 2001 at SUNY Oswego. It is basically an introduction to various polyhedra with an emphases on how the Jitterbug can be used to define all the polyhedra presented. (Best to use I.E. for viewing. Images are low quality for size constraint reasons.)

Here is the Pattern knot rotating around on a torus.

Here is show that 2 120 Polyhedra intersecting each other define 2 Vesica Pisces at 90 degrees to each other.

I have been studying the various ways of scaling the 120 Polyhedron. Might lead to some understanding of the fractal nature of the polyhedra and possible "harmonics" of space???

Here is one way of constructing the Pattern knot from 3 rings.

Another construction of the Pattern knot from 3 rings.

Here is one possibility for the creation of a 180 triangular faced polyhedron.

We are looking for a way that the Pattern knot can be dynamically genrated. Here is a possible Pattern knot (maybe) formed by the vertices of the 5 Octahedra. Recall that each Octahedron may be a Jitterbug.

A picture of the 120 Polyhedron with lots of other polyhedra in it.

Exploring the rotation of 4 Cubes plus 1 stationary cube. One position of the 5 cubes corresponds to a rhombuc Dodecahedron.

	"What's in this Polyhedron?" - An article I wrote exploring the 120 Polyhedron. This article includes the coordinates to the 62 vertices of the 120 Polyhedron. Shows the importance of the Golden Mean (a.k.a. Golden Ratio) to the 120 Polyhedron.
	Here is an animation showing the Jitterbug defining 3 rings (approximately). Could these 3 rings be the 3 rings of the Pattern Knot?
	Here are some interesting images I created while playing with the geometry.
	At one point in time, I started looking at various orientations of the 144 Polyhedron in a globe. The idea was to see if any of the vertices and edges matched up with the "World Grid" or "Sacred Sites". I am not particularly interested in this subject, but I thought I'd take a quick look see.
	Here is a "New Cosmic Heirarchy" model I am working on as well as some speculative application in physics. The model shown is that of the 144 Polyhedron using the FCC lattice.
	Here is a new movie of the 144 polyhedron and the Pattern Knot around it opening into its tetrahedron position. Note: This is not what Lynnclaire means by "the knot breathing."
	Here is a new construction method for the 120 polyhedron. It is based on using the Cube, Octahedron, Dodecahedron and Icosahedron.
	Here the Pattern Knot is drawn on the edges of the VE.
	Here is a way to construct the pattern on a tetrahedron.
	The "pattern" and the octahedron...
	The "pattern" and the Icosahedron...
	The "pattern" flexing from circles to tetrahedron position.
	I have developed some equations for drawing and analyzing the pattern.
	Comments on the Pattern Knot's motion.
	The pattern generates the duo-tetrahedron.
	The "pattern" divides (multiplies) into a higher octave.
	Here are some GIF movies showing the knot/pattern on a torus.
	Interactive viewer for the pattern.
	The "pattern" seen in crop circles?
	My explorations into the 144 polyhedron (the inner most polyhedron).
	The closest packing of spheres approach to the 144 polyhedron.
	The emergence of 4-fold symmertry from the 5-fold symmetry great circles of the Icosahedron.
	"Cut-out" patterns to build the 144 Polyhedron.
	Here is a newspaper article about a group of people investigating Lynnclaire's pattern and its potential significance.
	Is there a connection between the structure of the vacuum and electrodynamics?
	Information about the 144 polyhedron.
	Information about the 120 polyhedron.

Here are some links to interesting physical models of the "elementary" particles, nucleus, atoms, molecules, Universe.

Usage Note: My work is copyrighted. You may use my work but you may not include my work, or parts of it, in any for-profit project without my consent.