 Plurality of Inherent Topological Twonesses
Plurality of Inherent Topological Twonesses
1070.00  Plurality of Inherent Topological Twonesses
Plurality of Inherent Topological Twonesses
[1070.00-1077.11 Geometry of Two Scenario]

|
1071.00
 Systematic Character of Prime Thinkability
Systematic Character of Prime Thinkability
|

|
1071.10
 Prime: Prime means sizeless, timeless, subfrequency.
Prime is
prehierarchical. Prime is prefrequency. Prime is generalized,
a metaphysical
conceptualization experience, not a special case.
Prime: Prime means sizeless, timeless, subfrequency.
Prime is
prehierarchical. Prime is prefrequency. Prime is generalized,
a metaphysical
conceptualization experience, not a special case.
|

|
1071.20
 Systematic Realization: The mathematician's "purely
imaginative," no-
thickness, no breadth__ergo, no insideness or outsideness__
points, lines, and planes are
nonexperienceable. All image-ing derives from experience.
Conceptually imaginable point,
line, and plane experiences are only systemic__i.e.,
they have polyhedral insideness,
outsideness, and angular constancy independent of size.
Systematic Realization: The mathematician's "purely
imaginative," no-
thickness, no breadth__ergo, no insideness or outsideness__
points, lines, and planes are
nonexperienceable. All image-ing derives from experience.
Conceptually imaginable point,
line, and plane experiences are only systemic__i.e.,
they have polyhedral insideness,
outsideness, and angular constancy independent of size.
|

|
1071.21
 Size is always special case realizability. The mathematician's
undemonstrable
assumption that three points define a plane of no thickness__
no radial depth__is therefore
subsystemic; ergo, unthinkable, nonoperationally evidencible,
and unimaginable; ergo,
unemployable as constituents of proofs.
Size is always special case realizability. The mathematician's
undemonstrable
assumption that three points define a plane of no thickness__
no radial depth__is therefore
subsystemic; ergo, unthinkable, nonoperationally evidencible,
and unimaginable; ergo,
unemployable as constituents of proofs.
|

|
1071.22
 Contrary to conventional mathematical dogma three points
do not define a
nonexistent__ergo, nondemonstrable__no-thickness plane;
nor do they define an
altitudeless triangle because there can be naught to
do the defining systematically. No-
thickness is neither experimentally evidencible nor
conceptually feasible. System is
conceptual independent of size and special case.
Contrary to conventional mathematical dogma three points
do not define a
nonexistent__ergo, nondemonstrable__no-thickness plane;
nor do they define an
altitudeless triangle because there can be naught to
do the defining systematically. No-
thickness is neither experimentally evidencible nor
conceptually feasible. System is
conceptual independent of size and special case.
|

|
1071.23
 Operationally omnitriangulated polyhedra may be realized
only
systematically__i.e., with special case dimensionality
or special case radial depth of
insideness. Dimensionality = special case time-size
radial depth = frequency.
Operationally omnitriangulated polyhedra may be realized
only
systematically__i.e., with special case dimensionality
or special case radial depth of
insideness. Dimensionality = special case time-size
radial depth = frequency.
|

|
1071.24
 Radial depth is expressed in frequency of omnidirectional
wave propagations
per unit of time.
Radial depth is expressed in frequency of omnidirectional
wave propagations
per unit of time.
|

|
1071.25
 It takes a minimum of four differentially experienceable
event-loci to define a
system. System is primitively fourfoldedly experienceable.
When humans see three stars,
they see three separate special case events: there is
neither special case measurability nor
generalized considerability. With inherent a priori
systemic fourfoldedness there is
imaginability of topological vertexes and a sixfoldedness
of unique interrelatedness of the
inside-from-outside differentiating thinkability. Conceptual
= imaginable.
It takes a minimum of four differentially experienceable
event-loci to define a
system. System is primitively fourfoldedly experienceable.
When humans see three stars,
they see three separate special case events: there is
neither special case measurability nor
generalized considerability. With inherent a priori
systemic fourfoldedness there is
imaginability of topological vertexes and a sixfoldedness
of unique interrelatedness of the
inside-from-outside differentiating thinkability. Conceptual
= imaginable.
|

|
1071.26
 Prime thinkability is inherently systemic. Prime epistemology
is generalized
thinkability. Epistemology discovers intuition.
Prime thinkability is inherently systemic. Prime epistemology
is generalized
thinkability. Epistemology discovers intuition.
|

|
1071.27
 Intuition is the dawning awareness of the experienced,
but at first
unconsidered, newly occurring, unique, system-defining
fourfoldedness apprehending and
the epistemological system search for the sixfolded
system interrelationships.
Comprehension, often misidentified as "understanding,"
occurs when the six prehending
interattractive relationships of the fourfoldedness
are identified.
Intuition is the dawning awareness of the experienced,
but at first
unconsidered, newly occurring, unique, system-defining
fourfoldedness apprehending and
the epistemological system search for the sixfolded
system interrelationships.
Comprehension, often misidentified as "understanding,"
occurs when the six prehending
interattractive relationships of the fourfoldedness
are identified.
|

|
1071.28
 Structures are systems and have radial depth; wherefore
"surface" triangle
structures are always tetrahedra or truncated tetrahedra.
Structures are systems and have radial depth; wherefore
"surface" triangle
structures are always tetrahedra or truncated tetrahedra.
|

|
1072.00
 Definability of Structural Systems
Definability of Structural Systems
|

|
1072.10
 Proposition to Be Proven: that structural systems are
always special case
operational realizations in which there is a constant
relative abundance of all the
topological and system characteristics, the only variable
being a quantity multiplier
consisting of one of the first four prime numbers__1,
2, 3, and 5__or an intermultiplied
plurality of the same first four prime numbers.
Proposition to Be Proven: that structural systems are
always special case
operational realizations in which there is a constant
relative abundance of all the
topological and system characteristics, the only variable
being a quantity multiplier
consisting of one of the first four prime numbers__1,
2, 3, and 5__or an intermultiplied
plurality of the same first four prime numbers.
|

|
1072.11

Given: definition of prime: Sec. 1071.10 Given: definition of system: Sec. 400.01 Given: definition of structure: Sec. 600.02 Given: definition of structural systems: Sec. 610.20 Given: definition of prime tetra, octa, and icosa: Sec. 1011.30 Given: definition of subfrequency: Sec. 1011.32 Given: definition of nucleus: Secs. 414 and 1012.01 Given: definition of thinkable generalization: Sec. 501 Given: definition of special case realizations: Sec. 504 Given: definition of cosmic inherency: Sec. 1073 Given: definition of two kinds of twoness: Sec. 223.05 |

|
1072.20
 Generalized Topological Definability
Generalized Topological Definability
|

|
1072.21
 Generalized principles have topological system definability
of angle, number,
and constancy. Special cases have unique frequency dimensionability.
Wherefore we
propose that all recallably thinkable experiencings,
physical and metaphysical, are
fivefoldedly characterized:
Generalized principles have topological system definability
of angle, number,
and constancy. Special cases have unique frequency dimensionability.
Wherefore we
propose that all recallably thinkable experiencings,
physical and metaphysical, are
fivefoldedly characterized:

|

|
1072.22
 All conceptually thinkable, exclusively metaphysical
experiencings are
fourfoldedly characterized as above. All generalized
principles are conceptually thinkable
and fourfoldly definable. Generalization is conceptually
(i.e., systematically) imaginable
independent of (5) frequency.
All conceptually thinkable, exclusively metaphysical
experiencings are
fourfoldedly characterized as above. All generalized
principles are conceptually thinkable
and fourfoldly definable. Generalization is conceptually
(i.e., systematically) imaginable
independent of (5) frequency.
|

|
1072.23
 The fifth characteristic, frequency, is the unique
special case variable.
Physical experiencings are dependent not only on the
four generalizable characteristics,
but also on the fifth, frequency (i.e., size).
The fifth characteristic, frequency, is the unique
special case variable.
Physical experiencings are dependent not only on the
four generalizable characteristics,
but also on the fifth, frequency (i.e., size).
|

|
1072.30
 Wave and Particle Definability
Wave and Particle Definability
|

|
1072.31
 Wave as a constant topological aspect is exclusively
defined by angle,
conceptually independent of frequency; ergo, frequency
is the additional special case fifth
characteristic__the generalization realized in time.
Wave as a constant topological aspect is exclusively
defined by angle,
conceptually independent of frequency; ergo, frequency
is the additional special case fifth
characteristic__the generalization realized in time.
|

|
1072.32
 Particle is frequency-definable special case, and wave
is angularly defined
generalization. The numerically unique condition of
special case 5 (not equal) 4 of generalizations
identifies the dilemma of physics in reconciling the
minimum fourfoldedness of wave
definability by angles and the minimum fivefoldedness11
definability of particle
particularization by unique frequencies. (See Secs.
541.30,
961.46,
973.30, and
986.720).
Particle is frequency-definable special case, and wave
is angularly defined
generalization. The numerically unique condition of
special case 5 (not equal) 4 of generalizations
identifies the dilemma of physics in reconciling the
minimum fourfoldedness of wave
definability by angles and the minimum fivefoldedness11
definability of particle
particularization by unique frequencies. (See Secs.
541.30,
961.46,
973.30, and
986.720).
(Footnote 11: See Sec. 1053.12-15.) |

|
1073.00
 Cosmic Inherency
Cosmic Inherency
|
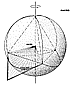 Fig. 1073.10 |
1073.10
 Four Kinds of Twoness
Four Kinds of Twoness
|

|
1073.11
 Since unity is plural and, at minimum, two, the additive
twoness of systemic
independence of the individual system's spinnability's
two axial poles, the latter's additive
twoness must be added to something, which thinkable
somethingness is the inherent
systemic multiplicative twoness of all systems' congruent
concave-convex inside-outness:
this additive-two-plus-multiplicative-two fourness inherently
produces the interrelationship
2 + 2 + 2 sixness (threefold twoness) of all minimum
structural-system comprehendibility.
Since unity is plural and, at minimum, two, the additive
twoness of systemic
independence of the individual system's spinnability's
two axial poles, the latter's additive
twoness must be added to something, which thinkable
somethingness is the inherent
systemic multiplicative twoness of all systems' congruent
concave-convex inside-outness:
this additive-two-plus-multiplicative-two fourness inherently
produces the interrelationship
2 + 2 + 2 sixness (threefold twoness) of all minimum
structural-system comprehendibility.
|

|
1073.12
 All systems are conceptually differentiated out of
Universe.
All systems are conceptually differentiated out of
Universe.
 System + environment = Universe System + environment = Universe
 Universe - system = environment Universe - system = environment
|

|
1073.13
 The environment is dual, consisting of the macro and
micro (outsideness and
insideness). Ergo, a fourth twoness of all prime structural
systems is synergetically
accountable as
The environment is dual, consisting of the macro and
micro (outsideness and
insideness). Ergo, a fourth twoness of all prime structural
systems is synergetically
accountable as
2 + 2 + 2 + 2 = 8.
(See Fig. 1073.10.) |

|
1073.14

Integral system is threefold twoness = 6. Integral Universe is fourfold twoness = 8.
|

|
1073.15
 The Indispensable Center: At the indispensable center
of the system
convergent-divergent Universe turns itself inside out.
The invisible, a priori, multiplicative
twoness differentially disclosed in the system's omnitopological
hierarchy is manifest of
the integrity of the sizeless, timeless nonconceptuality
always complementing the
conceptual system takeout from nonconceptual Scenario
Universe's eternal regenerating.
(See Sec.
1006.10.)
The Indispensable Center: At the indispensable center
of the system
convergent-divergent Universe turns itself inside out.
The invisible, a priori, multiplicative
twoness differentially disclosed in the system's omnitopological
hierarchy is manifest of
the integrity of the sizeless, timeless nonconceptuality
always complementing the
conceptual system takeout from nonconceptual Scenario
Universe's eternal regenerating.
(See Sec.
1006.10.)
|

|
1073.16
 Partial vacuum results as the physical atmospheric
gases are removed;
beyond those zero evacuations the electromagnetic tensing
induces reverse flows of
physically demonstrable positive energy (as manifest
in cryogenics, in which liquids flow
antigravitationally). Vacuum = novent.
Partial vacuum results as the physical atmospheric
gases are removed;
beyond those zero evacuations the electromagnetic tensing
induces reverse flows of
physically demonstrable positive energy (as manifest
in cryogenics, in which liquids flow
antigravitationally). Vacuum = novent.
|

|
1073.20
 Interrelationship Twoness: Third Kind of Twoness
Interrelationship Twoness: Third Kind of Twoness
|

|
1073.21
 All systems have a neutral axis of spinnability, with
two external polar
vertexes and two interior center axis vertexes which
are congruent__ ergo, visible only as
one vertex located at the convergence-divergence, integrative-disintegrative,
inbound-
outbound, turnaround, neutral center of gravity-center
of radiation of the system.
All systems have a neutral axis of spinnability, with
two external polar
vertexes and two interior center axis vertexes which
are congruent__ ergo, visible only as
one vertex located at the convergence-divergence, integrative-disintegrative,
inbound-
outbound, turnaround, neutral center of gravity-center
of radiation of the system.
|

|
1073.22
 The exterior and separate set of two polar vertexes
is the additive twoness of
systems, and the congruent exterior-interior set is
the multiplicative twoness of all
systems. The interior-exterior differentiating fourness
has an interrelated sixness that
differentiates as a unique third kind of twoness of
unique interrelatedness of all systems.
The exterior and separate set of two polar vertexes
is the additive twoness of
systems, and the congruent exterior-interior set is
the multiplicative twoness of all
systems. The interior-exterior differentiating fourness
has an interrelated sixness that
differentiates as a unique third kind of twoness of
unique interrelatedness of all systems.
|

|
1074.00
 Prime Nuclear Structural Systems
Prime Nuclear Structural Systems
|

|
1074.10
 All prime nuclear structural systems have one__and only
one__ (unity two)
interior vertex.
All prime nuclear structural systems have one__and only
one__ (unity two)
interior vertex.
|

|
1074.11
 Internally nuclear structural systems internally consist
entirely of tetrahedra
that have only one common interior vertex: omniconvertex.
Internally nuclear structural systems internally consist
entirely of tetrahedra
that have only one common interior vertex: omniconvertex.
|

|
1074.12
 In nuclear structural systems each of the surface system's
external triangles
constitutes the single exterior facet of an omnisystem-occupying
set of inter-triple-bonded
tetrahedra, each of whose single interior-to-system
vertexes are congruent with one
another at the convergent nuclear center of the system.
In nuclear structural systems each of the surface system's
external triangles
constitutes the single exterior facet of an omnisystem-occupying
set of inter-triple-bonded
tetrahedra, each of whose single interior-to-system
vertexes are congruent with one
another at the convergent nuclear center of the system.
|
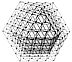 Fig. 1074.13 |
1074.13
 In all nonredundant, prime, nuclear structural systems
the congruently
interior-vertexed, omnisystem-occupying tetrahedra of
all prime structural systems may all
be interiorly truncated by introducing special-case
frequency, which provides chordal as
well as radial modular subdivisioning of the isotropic-vector-matrix
intertriangulation of
each radial, frequency-embracing wave layer, always
accomplished while sustaining the
structural rigidity of the system. (See Fig.
1074.13.)
In all nonredundant, prime, nuclear structural systems
the congruently
interior-vertexed, omnisystem-occupying tetrahedra of
all prime structural systems may all
be interiorly truncated by introducing special-case
frequency, which provides chordal as
well as radial modular subdivisioning of the isotropic-vector-matrix
intertriangulation of
each radial, frequency-embracing wave layer, always
accomplished while sustaining the
structural rigidity of the system. (See Fig.
1074.13.)
|

|
1074.20
 Omnitopological Domains
Omnitopological Domains
|

|
1074.21
 Omnitopological domains are defined in terms of the
system's unique
central-angle-defined insideness and its unique surface-angle-defined
outsideness. (See
Sec.
1006.20.)
Omnitopological domains are defined in terms of the
system's unique
central-angle-defined insideness and its unique surface-angle-defined
outsideness. (See
Sec.
1006.20.)
|

|
1074.30
 Spin Twoness and Duality Twoness
Spin Twoness and Duality Twoness
|

|
1074.31
 Having identified (a) the constant additive twoness
of the vertexial poles of
the axial spinnability operative in all independent
systems, and (b) the multiplicative
twoness characterizing the concavity and convexity congruently
operative in all
independent systems, we find that the first four prime
numbers__1, 2, 3, and 5__are the
only variables present in the Eulerean topological inventorying
of all the omnitriangularly,
nonredundantly stabilized, symmetrical polyhedra.
Having identified (a) the constant additive twoness
of the vertexial poles of
the axial spinnability operative in all independent
systems, and (b) the multiplicative
twoness characterizing the concavity and convexity congruently
operative in all
independent systems, we find that the first four prime
numbers__1, 2, 3, and 5__are the
only variables present in the Eulerean topological inventorying
of all the omnitriangularly,
nonredundantly stabilized, symmetrical polyhedra.
|

|
1074.32

|

|
1075.00
 Special Case: Energy and Information
Special Case: Energy and Information
|

|
1075.10
 Structures are always special case. Structures are
operational. Operational =
physically realized. Structures always have unique size.
By definition a structure is a
complex of energy events interacting to produce a stable
pattern.
Structures are always special case. Structures are
operational. Operational =
physically realized. Structures always have unique size.
By definition a structure is a
complex of energy events interacting to produce a stable
pattern.
|

|
1075.11
 An energy event is always special case. Whenever we
have experienced
energy, we have special case. The physicist's first
definition of physical is that it is an
experience that is extracorporeally, remotely, instrumentally
apprehensible. Metaphysical
includes all the experiences that are excluded by the
definition of physical. Metaphysical is
always generalized principle .
An energy event is always special case. Whenever we
have experienced
energy, we have special case. The physicist's first
definition of physical is that it is an
experience that is extracorporeally, remotely, instrumentally
apprehensible. Metaphysical
includes all the experiences that are excluded by the
definition of physical. Metaphysical is
always generalized principle .
|

|
1075.12
 Physical is always special case. Energy is physical
and always special case.
Information is always special case. Energy is information:
information is energy. Special
case is always realized by its energetic information
Dimension is unique frequency
information. Time incrementation is special case information.
Concept is general:
information is quantitative (special case) .
Physical is always special case. Energy is physical
and always special case.
Information is always special case. Energy is information:
information is energy. Special
case is always realized by its energetic information
Dimension is unique frequency
information. Time incrementation is special case information.
Concept is general:
information is quantitative (special case) .
|

|
1075.20
 Equation of Intellect
Equation of Intellect
|

|
1075.21
 By thermodynamic law energy may neither be created
nor lost in Universe.
By synergetic postulate intellect is irrevocable and
irreversibly comprehensive__both
subjectively and objectively__in respect to energy.
By thermodynamic law energy may neither be created
nor lost in Universe.
By synergetic postulate intellect is irrevocable and
irreversibly comprehensive__both
subjectively and objectively__in respect to energy.
|

|
1075.22
 Intellect mensurates and modulates relative energy
events and event
interrelationships. The total quantity of energy operative
in Universe is a constant, but a
dependent, function of intellect. Universe is the integral
of all metaphysical and physical
phenomena.
Intellect mensurates and modulates relative energy
events and event
interrelationships. The total quantity of energy operative
in Universe is a constant, but a
dependent, function of intellect. Universe is the integral
of all metaphysical and physical
phenomena.
|

|
1075.23
 In respect to individual humans total energy occurs
as a complex of local
variables of systematically cooperative, convergent-divergent,
complementary-reciprocal,
intertransformation patternings of uniquely differentiable
local system aspects, accountable
by intellect in locally varying magnitudes of concentration.
The modulations are selectable,
predictable, and governable by intellect to the extent
that superficial acceleration permits.
In respect to individual humans total energy occurs
as a complex of local
variables of systematically cooperative, convergent-divergent,
complementary-reciprocal,
intertransformation patternings of uniquely differentiable
local system aspects, accountable
by intellect in locally varying magnitudes of concentration.
The modulations are selectable,
predictable, and governable by intellect to the extent
that superficial acceleration permits.
|

|
1075.24
 Modulations through local transformations are arranged
or valved by
intellect through inherent associative-disassociative
patterning of local energy-complex
environments. Thus the aggregate effective energy behavior
sum-totally accountable as a
universal constant is engaged in its local behaviors
by individual experience (and
apprehended and appraised by consciously operative intellect)
in widely differentiated sets
of patterns in variable magnitudes of regenerative pattern
concentrations.
Modulations through local transformations are arranged
or valved by
intellect through inherent associative-disassociative
patterning of local energy-complex
environments. Thus the aggregate effective energy behavior
sum-totally accountable as a
universal constant is engaged in its local behaviors
by individual experience (and
apprehended and appraised by consciously operative intellect)
in widely differentiated sets
of patterns in variable magnitudes of regenerative pattern
concentrations.
|

|
1075.25
 Wealth is the measurable degree of established operative
advantage locally
organized by generalized-principle-employing intellect
over the locally occurring,
differentiable behaviors of universal energy. Wealth
is an irreversible advantage: it cannot
be expended in a preferred reorganization of past events;
it can only be expended in
organizing forward events in preferential patterns.
Wealth is the measurable degree of established operative
advantage locally
organized by generalized-principle-employing intellect
over the locally occurring,
differentiable behaviors of universal energy. Wealth
is an irreversible advantage: it cannot
be expended in a preferred reorganization of past events;
it can only be expended in
organizing forward events in preferential patterns.
|

|
1075.26
 The wealth advantage increases as intellect comprehends
local behaviors and
acts in complementary regeneration to produce patterns
advantageous to human
processes. With every inventorying of local-energy behaviors
by intellect, and with the
informed rearrangement of them to provide wider, more
frequently and precisely
modulatable patterns with ever less weight of materials
ergo of energy__and fewer
seconds of time per accomplished life protection, support,
and accommodation function,
the established wealth advantage is manifest and the
documented knowledge in local
Universe increases.
The wealth advantage increases as intellect comprehends
local behaviors and
acts in complementary regeneration to produce patterns
advantageous to human
processes. With every inventorying of local-energy behaviors
by intellect, and with the
informed rearrangement of them to provide wider, more
frequently and precisely
modulatable patterns with ever less weight of materials
ergo of energy__and fewer
seconds of time per accomplished life protection, support,
and accommodation function,
the established wealth advantage is manifest and the
documented knowledge in local
Universe increases.
|

|
1076.00
 Primitive Regeneration
Primitive Regeneration
|

|
1076.10
 Prime = primitive. Primitive is generalized principle
and not special case.
Virgin = primitive. "Virgin soil" = special case. Virgin
female human = special case, only
because of the "human" case realization. Virginity is
a generalized aspect of primitive.
There can be no special-case generalized virgins. Virginity
is not only prefrequency, it is
pretime, pre-special-case, and pre-experienceable-dimension.
Prime = primitive. Primitive is generalized principle
and not special case.
Virgin = primitive. "Virgin soil" = special case. Virgin
female human = special case, only
because of the "human" case realization. Virginity is
a generalized aspect of primitive.
There can be no special-case generalized virgins. Virginity
is not only prefrequency, it is
pretime, pre-special-case, and pre-experienceable-dimension.
|

|
1076.11
 Virgin identifies the topological insideness aspect
of the coincidental
insideness-outsideness of all generalized systems independently
differentiated from all the
macrocosmos Universe outside the virginal system, from
all the microcosm Universe
inside the virginal system and from the little of the
cosmos Universe with which the virgin
imaginably differentiates the outsideness from the insideness.
And virgin is half a system
because unity is plural and at minimum two, the virgin
being the prime insideness of
concavity to be dimensionally or experientially and
operationally realized only by special-
case-recognized congruence of the convex outsideness
with the inside concavity.
Virgin identifies the topological insideness aspect
of the coincidental
insideness-outsideness of all generalized systems independently
differentiated from all the
macrocosmos Universe outside the virginal system, from
all the microcosm Universe
inside the virginal system and from the little of the
cosmos Universe with which the virgin
imaginably differentiates the outsideness from the insideness.
And virgin is half a system
because unity is plural and at minimum two, the virgin
being the prime insideness of
concavity to be dimensionally or experientially and
operationally realized only by special-
case-recognized congruence of the convex outsideness
with the inside concavity.
|

|
1076.12

Engendering is a special-case phenomenon that requires fertilization. Fertilization is the systemic differentiating out of Universe that produces conceptually local Universe marrying the macrocosm to the microcosm, which realizes a new special-case system event with its own set of insideness-outsideness topological characteristics. |

|
1076.13
 Physics of the 1970s identifies:
Physics of the 1970s identifies:
2 quantum = 1/2 spin; and 1 quantum = 2 (spin/2)
Conception-birth comes with the realization that the aspects of the externally viewed, plus-curvature convexity that are seemingly separate from those of the internally viewed, minus-curvature concavity have no interveningly differentiating, zero-curvature sheath structurally differentiating the only timelessly (or generalized) conceptual coincidence of both the plus and minus curvature. In the alternately plus-or-minus pulsativeness frequencies of special case time the multiplicative twoness "conception" releases or gives birth to new, coexistent, additive twonesses as independently axially spinnable: special case spin twoness inherently coupled with the duality twoness, producing the individual unity fourness, with its primitive sixfoldedness of integral system interrelatedness and its eightfolded integral Universe environment. |

|
1077.00
 Prime Number Inherency and Constant Relative Abundance
Prime Number Inherency and Constant Relative Abundance
|

|
1077.10
 Since the relative interabundance of one nonspin vertex
for every two faces
and every three edges is a constant topological system
condition, we may identify them as
a constant interabundance set in terms of the number
of vertexes and edges as a constant
topological relationship of all symmetrical and triangularly
stabilized, modularly
unsubdivided, polyhedral systems.
Since the relative interabundance of one nonspin vertex
for every two faces
and every three edges is a constant topological system
condition, we may identify them as
a constant interabundance set in terms of the number
of vertexes and edges as a constant
topological relationship of all symmetrical and triangularly
stabilized, modularly
unsubdivided, polyhedral systems.
|

|
1077.11
 We may substitute T, meaning the number of topological
system sets, for the
bracketed groups:
We may substitute T, meaning the number of topological
system sets, for the
bracketed groups:
.: 2 + 2 = T.
And when the symmetrical, omninonredundantly triangulated,
modularly unsubdivided
systems are subjected to symmetrical modular subdivision,
and the number of edge-
module subdivisions is represented by F, then:
2 + 2NF2 = T.
where the first 2 is the additive spin two; the second
2 is the multiplicative duality two; N
is the prime number uniquely characterizing the system;
F is the frequency of modular
subdividing; and T is the number of topological sets
of one vertex plus two faces equal
three edges (1 + 2 = 3) that exists in the symmetrical
structural (because nonredundant)
triangulated polyhedral system. Q.E.D.: See Sec.
223.
|
| Next Chapter: 1100.00 |